 Author
Author |
Topic: Complex powers (Read 1907 times) |
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Complex powers
« on: Sep 18th, 2007, 10:14pm » |
 Quote Quote  Modify Modify
|
If ii^i... = A + = A + 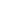 B, then find B, then find
1) tan( A/2) A/2)
2) A2 + B2
Note: How do you do multiple sup? The question above is i^i^i...
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
JP05
Guest

|
Since your are asking does i^i = e^(-1/2 pi) or i^i = (-1)^ (1/2 i)? That is, for starters anyway.
|
| « Last Edit: Sep 18th, 2007, 10:37pm by JP05 » |
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Complex powers
« Reply #2 on: Sep 18th, 2007, 10:46pm » |
 Quote Quote  Modify Modify
|
on Sep 18th, 2007, 10:35pm, JP05 wrote:| Since your are asking does i^i = e^(-1/2 pi) or i^i = (-1)^ (1/2 i)? That is, for starters anyway. |
|
Former.. Latter is not valid!! That would what a "certain individual" would do and give bad answers!! 
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
TenaliRaman
Uberpuzzler
    

I am no special. I am only passionately curious.
Gender: 
Posts: 1001
|
 |
Re: Complex powers
« Reply #3 on: Sep 18th, 2007, 10:51pm » |
 Quote Quote  Modify Modify
|
Bluntly,
x = i^x
log(x) = x log i
(1/2)(A^2 + B^2) + i arctan(A/B) = iA(pi/2) - B(pi/2)
tan(A(pi/2)) = A/B
A^2 + B^2 = -Bpi
Ofcourse, we could go further with x = W(-log(i))/log(i) and probably separate A and B as two series. Havent tried it, maybe it simplifies further.
|
|
 IP Logged IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
JP05
Guest

|
on Sep 18th, 2007, 10:46pm, Sameer wrote:
Former.. Latter is not valid!! That would what a "certain individual" would do and give bad answers!!  |
|
Really? That's not what I know about complex numbers. That is, both are valid.
|
| « Last Edit: Sep 18th, 2007, 11:00pm by JP05 » |
 IP Logged IP Logged |
|
|
|
JP05
Guest

|
As a follow up, I am not putting forth my remarks in reference to "any particular person" but I am simply being as precise mathematically as I know how. In this end, i^i = (-1)^(1/2 i) is precise in one of a number of ways i^i can be wrote.
|
|
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Complex powers
« Reply #6 on: Sep 18th, 2007, 11:07pm » |
 Quote Quote  Modify Modify
|
on Sep 18th, 2007, 10:51pm, TenaliRaman wrote:Bluntly,
x = i^x
log(x) = x log i
(1/2)(A^2 + B^2) + i arctan(A/B) = iA(pi/2) - B(pi/2)
tan(A(pi/2)) = A/B
A^2 + B^2 = -Bpi
Ofcourse, we could go further with x = W(-log(i))/log(i) and probably separate A and B as two series. Havent tried it, maybe it simplifies further.
|
|
For 1) I actually have the inverse!! And for 2) I have your answer on an exponent!!
Note: Alright, these look like easy problems.. I will move to the next chapter in my book!! 
on Sep 18th, 2007, 11:06pm, JP05 wrote:As a follow up, I am not putting forth my remarks in reference to "any particular person" but I am simply being as precise mathematically as I know how. In this end, i^i = (-1)^(1/2 i) is precise in one of a number of ways i^i can be wrote.
|
|
Ah don't worry about that. It was my feeble attempt at being funny which came across terribly. I am not sure this representation is legal unless someone here can correct me or support me!!
Edit: -1 = ei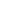 implies both are same things!! So you should be able to use either!! (So both are legal) implies both are same things!! So you should be able to use either!! (So both are legal)
|
| « Last Edit: Sep 19th, 2007, 6:50pm by Sameer » |
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
JP05
Guest

|
There is often a lot of nonsense when it comes to complex numbers and it simply has to do with the fact they they are, well, complex, and really don't play out like we expect real numbers to. In fact, over time you will discover what I just said the hard way.
So, someone give us a limit for that infinite complex exponentiation so we can put this thing to bed. I am looking for a limit -- that is, at least we can have one-sided continuity.
|
|
 IP Logged IP Logged |
|
|
|
JP05
Guest

|
Dont write -1 = e^pi because -1 has other representations besides e^pi. I have seen mathematicians write stuff like that but they were being funny at the time.
Say, e^pi = -1.
|
|
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Complex powers
« Reply #9 on: Sep 18th, 2007, 11:33pm » |
 Quote Quote  Modify Modify
|
on Sep 18th, 2007, 11:31pm, JP05 wrote:Dont write -1 = e^pi because -1 has other representations besides e^pi. I have seen mathematicians write stuff like that but they were being funny at the time.
Say, e^pi = -1. |
|
Of course, I am an engineer so I tend to overlook these things...
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
JP05
Guest

|
Cool. I am still looking for that limit though. I would be pleased to work with it here if you can give me one, as 1 and 2 in this problem would be trivial.
The thing to consider is really what happens as you continue to exponentiate i, regardless if the exponents resolve to real or complex numbers ultimately. This is why I want to see that limit formula.
Well, there is one: how many shapes can it take: i or -1 ...huh? I know the answer!
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Complex powers
« Reply #11 on: Sep 19th, 2007, 6:14am » |
 Quote Quote  Modify Modify
|
When 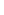 is exponentiated upwards n times (downwards is normal), it is alternately real or complex, depending on n. To say that it equals a + is exponentiated upwards n times (downwards is normal), it is alternately real or complex, depending on n. To say that it equals a + 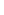 b when exponentiated an infinite number of times is to say that infinity is either odd or even! b when exponentiated an infinite number of times is to say that infinity is either odd or even!
|
| « Last Edit: Sep 19th, 2007, 9:54am by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Complex powers
« Reply #12 on: Sep 19th, 2007, 7:22am » |
 Quote Quote  Modify Modify
|
on Sep 19th, 2007, 6:14am, ThudanBlunder wrote:When 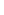 is exponentiated n times, it is alternately real or complex, depending on n. To say that it equals a + is exponentiated n times, it is alternately real or complex, depending on n. To say that it equals a + 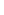 b when exponentiated an infinite number of times is to say that infinity is either odd or even! b when exponentiated an infinite number of times is to say that infinity is either odd or even! |
|
Unless it converged on 0.
(But it doesn't, does it?)
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Complex powers
« Reply #13 on: Sep 19th, 2007, 8:57am » |
 Quote Quote  Modify Modify
|
on Sep 19th, 2007, 7:22am, towr wrote:
Unless it converged on 0.
(But it doesn't, does it?) |
|
Doesn't the sequence repeat itself?
e- /2 to the power of /2 to the power of 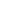 = =  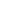 , right? , right?
|
| « Last Edit: Sep 19th, 2007, 12:04pm by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Complex powers
« Reply #14 on: Sep 19th, 2007, 6:20pm » |
 Quote Quote  Modify Modify
|
You don't need to find A and B by themselves...
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Complex powers
« Reply #16 on: Sep 19th, 2007, 6:53pm » |
 Quote Quote  Modify Modify
|
on Sep 19th, 2007, 6:36pm, srn347 wrote:| How do you apply complex powers? I'm only familiar with e being the base when there are complex powers(or 1 which is still 1 always). |
|
You can use the fact that e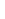 2k 2k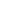 = 1 = 1
This is a little beyond high school math. You would want to pick a book that has a chapter on complex numbers, Argand's diagram, De Moivre's theorem, hyperbolics, etc. That would help!
on Sep 19th, 2007, 6:36pm, srn347 wrote:
Corrected!
|
| « Last Edit: Sep 19th, 2007, 6:57pm by Sameer » |
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: Complex powers
« Reply #17 on: Sep 19th, 2007, 10:29pm » |
 Quote Quote  Modify Modify
|
that is something I already understand. How do I apply complex powers to something that isn't e(or 1)?
|
| « Last Edit: Sep 19th, 2007, 10:31pm by srn437 » |
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Complex powers
« Reply #18 on: Sep 19th, 2007, 11:00pm » |
 Quote Quote  Modify Modify
|
on Sep 19th, 2007, 10:29pm, srn347 wrote:| that is something I already understand. How do I apply complex powers to something that isn't e(or 1)? |
|
I am not sure I understand the source of your confusion. A complex number can be expressed as re 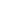
A complex number can be thought up as a point in a z plane, thus expressable in terms of distance from origin and angle from positive x axis.
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7528
|
 |
Re: Complex powers
« Reply #19 on: Sep 20th, 2007, 7:08am » |
 Quote Quote  Modify Modify
|
on Sep 19th, 2007, 10:29pm, srn347 wrote:| How do I apply complex powers to something that isn't e(or 1)? |
|
Let's take xy
If y is an integer, you can define it as successive multiplications. If x is e, you can define it as exp(x) where the exp() function is defined as
exp(x) = sum(xn/n!)
In the general case
xy = exp(y·ln(x)).
where the ln() function is the inverse of the exp() function.
The problem in the general case is that the solution to
exp(z) = x
is not unique for a given x. If z is a solution,
z' = z + i·k·2·pi
is also a solution. If y is integer it doesn't matter, the different solutions fold back to a single value after applying exp(). If y is rational, y=p/q, the solutions fold back to q distinct values. In the general case there can be an infinity of values, and you have to choose one.
Out of my head, I cannot think of an good use for complex exponents, except for the case ez which is just a way to write the exp() function.
[Sorry, wrong button -Eigenray]
|
| « Last Edit: Sep 20th, 2007, 6:48pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
ThudnBlunder
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Complex powers
« Reply #20 on: Sep 20th, 2007, 8:16am » |
 Quote Quote  Modify Modify
|
on Sep 20th, 2007, 7:08am, Grimbal wrote:
Out of my head, I cannot think of an good use for complex exponents... |
|
Fourier Transforms?
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7528
|
 |
Re: Complex powers
« Reply #21 on: Sep 20th, 2007, 8:19am » |
 Quote Quote  Modify Modify
|
I meant other than the special case ez.
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Complex powers
« Reply #22 on: Sep 20th, 2007, 6:52pm » |
 Quote Quote  Modify Modify
|
on Sep 20th, 2007, 7:08am, Grimbal wrote:| Out of my head, I cannot think of an good use for complex exponents, except for the case ez which is just a way to write the exp() function. |
|
Dirichlet series.
Yes, it is pretty rare to see wz (unless z  , or w=e, or w , or w=e, or w 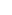 ), but this is probably because it is not well-defined. The whole point of common notation, after all, is that you don't have to define it every time you use it. ), but this is probably because it is not well-defined. The whole point of common notation, after all, is that you don't have to define it every time you use it.
[Argh! I accidentally replaced Grimbal's entire post with this one. Lucky I noticed before closing the tab! And this happened right after I posted about this very problem!!]
|
| « Last Edit: Sep 20th, 2007, 6:57pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: Complex powers
« Reply #23 on: Sep 26th, 2007, 7:27pm » |
 Quote Quote  Modify Modify
|
How do you define ni when n is not 1, -1, or or e to some power.
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7528
|
 |
Re: Complex powers
« Reply #24 on: Sep 27th, 2007, 12:28am » |
 Quote Quote  Modify Modify
|
on Sep 26th, 2007, 7:27pm, srn347 wrote:| How do you define ni when n is not 1, -1, or or e to some power. |
|
Just apply what I explained in post 19.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register