 Author
Author |
Topic: Extending Euler's Theorem (Read 1600 times) |
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Extending Euler's Theorem
« on: Oct 10th, 2007, 10:53am » |
 Quote Quote  Modify Modify
|
Not so much a puzzle as a question, I guess:
After my stumbling in this thread I've done a bit more experimenting and feel reasonably confident in the following two claims:
1) For all a  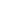 , m , m  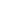 there exists some least nonnegative t there exists some least nonnegative t  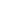 such that a such that a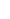 (m) + t (m) + t  at (mod m), where at (mod m), where  (m) is Euler's Totient Function. (m) is Euler's Totient Function.
2) If and only if GCD(a, m) = 1 then t = 0 (Euler's Theorem); otherwise t = max( Mi/Ai Mi/Ai ), where for prime factors p1, p2, ..., pn common to a and m, Mi is the multiplicity of pi in m and Ai is the multiplicity of pi in a. ), where for prime factors p1, p2, ..., pn common to a and m, Mi is the multiplicity of pi in m and Ai is the multiplicity of pi in a.
I have empirical evidence that no violation of those claims exists for 1  m m  2,500 25,000 80,000 250,000, and an intuitive feel for why they should be true, but no proof of either claim; nor have I been able to find a reference one way or the other. I'm wondering a) if this is a (well) known (or trivial) result that I'm just unable to find, and b) if anyone here has a proof (or, more interesting, a disproof).
--SMQ
|
| « Last Edit: Oct 11th, 2007, 11:23am by SMQ » |
 IP Logged IP Logged |
--SMQ
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Extending Euler's Theorem
« Reply #1 on: Oct 15th, 2007, 9:02am » |
 Quote Quote  Modify Modify
|
Interesting. I think your conjectures are true. Here is an analysis of an important special case which may be hopefully converted to a full proof.
Let gcd(a, m) be a power of a prime p. That is, a = rpi, m = spj, r, s, p are relatively prime. Let further d =  (s). Then, (rpi)d+1 = rpi mod s. That is, (rpi)d+1 - rpi = qs. Since p doesn’t divide s, it follows pi | q, and thus (rpi)d+1 = rpi mod spi. (s). Then, (rpi)d+1 = rpi mod s. That is, (rpi)d+1 - rpi = qs. Since p doesn’t divide s, it follows pi | q, and thus (rpi)d+1 = rpi mod spi.
Note also that pi+1 doesn’t divide q (otherwise p divides r, which is impossible). If j  i, we are done. Otherwise, (rpi)u(rpi)d+1 = rpu+1 mod spj, where u is the least integer such that ui i, we are done. Otherwise, (rpi)u(rpi)d+1 = rpu+1 mod spj, where u is the least integer such that ui  j – i. But this is exactly the condition stated by SMQ in the second claim. j – i. But this is exactly the condition stated by SMQ in the second claim.
Finally, because d |  (a), the first statement also follows. (a), the first statement also follows.
|
|
 IP Logged IP Logged |
|
|
|
Pietro K.C.
Full Member
  

 

Gender: 
Posts: 213
|
 |
Re: Extending Euler's Theorem
« Reply #2 on: Oct 17th, 2007, 12:21am » |
 Quote Quote  Modify Modify
|
That is an extremely interesting question.
Given a finite set S with a binary operation * defined on it, the "powers" of any given element s in S, ie
s, s², s³, ...
must eventually repeat some value. If sk is the first such repeated value, and sk+T the second occurrence, then the powers go around in a circle of size T thereafter:
sk <-- ... <-- s³ <-- s² <-- s
/ \
\ _ /
SMQ's question may thus be read as follows: is  (m) big enough to get out of the linear part above, and reach the loop? (If a power is in the loop, then there trivially exists your least t, since the natural numbers are well-ordered.) The answer is yes. (m) big enough to get out of the linear part above, and reach the loop? (If a power is in the loop, then there trivially exists your least t, since the natural numbers are well-ordered.) The answer is yes.
Let m=pr, and a=psb, with p a prime number and b coprime with p. It is trivial to check that, for integer k,
s>0 and k > r/s ---> ak=0 (mod m);
Also, for s>0,
 (m) = pr-1(p-1) >= 2r-1 >= r >= r/s. (m) = pr-1(p-1) >= 2r-1 >= r >= r/s.
This means that, unless p does not divide a, the "going to zero" tendency outruns the "repeat in a cycle" tendency: the only repeated value is 0.
Now all we need is Chinese Remainder to glue the local results together. Break down a given m into its prime power factors, recall that  is multiplicative across relatively prime numbers, and reason as follows. For each factor pr of m, either is multiplicative across relatively prime numbers, and reason as follows. For each factor pr of m, either
(i) p divides a, and, as we saw,  (pr) is a big enough power to reach 0 in the (mod pr)-loop, whence a (pr) is a big enough power to reach 0 in the (mod pr)-loop, whence a (m) = 0 (mod pr); (m) = 0 (mod pr);
(ii) p does not divide a, and the latter is therefore already in the loop of its generated subgroup in the multiplicative group of integers prime to pr.
Therefore, a (m) is in the (mod m)-loop of powers of a. As regards a specific value for t=T, it is easy from the above to see what is "really" going on: modulo primes in m not dividing a, the equation (m) is in the (mod m)-loop of powers of a. As regards a specific value for t=T, it is easy from the above to see what is "really" going on: modulo primes in m not dividing a, the equation
a (m)+t = at (m)+t = at
is true for every t; what is needed is some t high enough that at will be zero modulo those other primes. SMQ's formula is thus correct.
|
| « Last Edit: Oct 17th, 2007, 12:23am by Pietro K.C. » |
 IP Logged IP Logged |
"I always wondered about the meaning of life. So I looked it up in the dictionary under 'L' and there it was --- the meaning of life. It was not what I expected." (Dogbert)
|
|
|
cuckoo
Junior Member
 

Gender: 
Posts: 57
|
 |
Re: Extending Euler's Theorem
« Reply #3 on: Nov 7th, 2007, 1:27am » |
 Quote Quote  Modify Modify
|
Here is my proof:
let m = (p_1^M_1)*...*(p_s^M_s), then a^(\phi(m)+t)=a^t (mod m) is equivalent to
a^t * [a^\phi(m)-1] = 0 (mod p_i^M_i), for any 1<= i <=s.
if (p_i, a)=1, since \phi(m) is a multiple of \phi(p_i^M_i), so [a^\phi(m) -1] = 0 (mod p_i^M_i)
and the above equation holds forever;
if (p_i, a)>1, say the power index of p_i in a is A_i,
then we must have a^t = 0 (mod p_i^M_i). so we get : t*A_i >= M_i.
To conclude, we must have t >= max( ceil(M_i/A_i) ).
done.
|
| « Last Edit: Nov 7th, 2007, 1:31am by cuckoo » |
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register