wu :: forums « wu :: forums - tough number theory prob. » Welcome, Guest. Please Login or Register. Dec 1st, 2024, 12:31pm

RIDDLES SITE WRITE MATH! Home Help Search Members Login Register

wu :: forums    riddles    putnam exam (pure math) (Moderators: towr, william wu, SMQ, Icarus, Eigenray, Grimbal)    tough number theory prob. « Previous topic | Next topic » Pages: 1 2  Reply Notify of replies Send Topic Print    Author  Topic: tough number theory prob.  (Read 3031 times) LeoYard Newbie     Posts: 35 tough number theory prob.   « on: Jun 10th, 2008, 12:29pm » Quote Modify Let w=(-1 +(-3)^0.5))/2 and note that w^2=-1 -w.   Consider the integral domain Z +Zw, and let U(Z+Zw) be the set of units.     Prove that U(Z+Zw)=(+1,-1, +w, -w ,+w^2, -w^2).     Here's my next question:     Let m be an integer with m = 1 (mod 4) and m less than -3.   Prove that the set of units U(Z +Z((1 + sqrt(m)/2) = (+1, -1) IP Logged Aryabhatta Uberpuzzler     Gender: Posts: 1321 Re: tough number theory prob.   « Reply #1 on: Jun 10th, 2008, 12:33pm » Quote Modify Is this homework? IP Logged LeoYard Newbie     Posts: 35 Re: tough number theory prob.   « Reply #2 on: Jun 10th, 2008, 1:07pm » Quote Modify on Jun 10th, 2008, 12:33pm, Aryabhatta wrote: Is this homework?   Yes, i need some help to get me started.   I need to add:   For a given integral domain A (say), a member 'i' (say) of this set is called a unit if there exists another element 'j' (say) in A such that i*j=1.     We denote the set of all the units of A as U(A)     In the first question, I'm saying that the only units for the integral domain (Z +Zw) are +1, -1, +w and -w.     IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: tough number theory prob.   « Reply #3 on: Jun 10th, 2008, 1:31pm » Quote Modify What do you know about norms? IP Logged LeoYard Newbie     Posts: 35 Re: tough number theory prob.   « Reply #4 on: Jun 10th, 2008, 2:47pm » Quote Modify I'm a bit overwhelmed by algebraic number theory.   Quote: What do you know about norms?   I've started Field norm in algebraic number theory. I'm embarrassed to say that I don't know how to tackle this problem. IP Logged LeoYard Newbie     Posts: 35 Re: tough number theory prob.   « Reply #5 on: Jun 10th, 2008, 10:23pm » Quote Modify I don't know much about "norms". I'm on chapter 1. My book in chapter 9 defines them as follows:   If K is an algebraic number field of degree n, and 'r' is an element of K then the norm of 'r' is     f_1(r)*f_2(r)*.....*f_n(r)     where f_i: K to C (set of complex numbers) are the n distinct monomorphisms from K to C.     There isn't anything in chapter 1 of my text which discusses it, so i'm supposed to solve this without them. IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: tough number theory prob.   « Reply #6 on: Jun 11th, 2008, 8:21am » Quote Modify Suppose x*y = 1.  Here are two approaches:   1. What do you know about the norms of x and y?   2. If x=a+bw, y=c+dw, find c,d in terms of a,b.  When are these integers? IP Logged LeoYard Newbie     Posts: 35 Re: tough number theory prob.   « Reply #7 on: Jun 11th, 2008, 1:00pm » Quote Modify I'm going with approach #2   First if If x=a+bw, y=c+dw then 1 = x*y = (a +bw)(c +dw)= ac + (ad +bc)w + (bd)w^2.     Now w^2 = -w -1. Hence (ac) + (ad +bc)w + (bd)w^2 = (ac - bd) + (ad +bc -bd)w = 1     This implies that ac - bd = 1 and that ad +bc -bd = 0 (eg bd =ad +bc).     I'm not sure where it is I'm suppose to go from here. IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: tough number theory prob.   « Reply #8 on: Jun 11th, 2008, 3:27pm » Quote Modify You can solve the system of equations for c and d.  Or, you can just rationalize 1/(a+bw) = (a+bw2)/((a+bw)(a+bw2)).  You should find that a2-ab+b2 divides both b and a-b.  By considering gcd(a,b) you can show a2-ab+b2 = 1 (-1 is impossible).   It may be easier to express elements of Z[w] as (a + b(-3))/2 instead, where a,b are integers of the same parity.   Do you know how to show that 1, i are the only units of the Gaussian integers Z[i]?  The proof is much the same. « Last Edit: Jun 11th, 2008, 3:27pm by Eigenray » IP Logged LeoYard Newbie     Posts: 35 Re: tough number theory prob.   « Reply #9 on: Jun 11th, 2008, 11:12pm » Quote Modify Sorry but I'm afraid I couldn't follow your reasoning for much of any of that. Can you please show me either how it is you can solve for c and d, or the other procedure you suggested?       Yes I do know how to prove that the set of units for Z(i) is (+1, -1, +i, -i). It goes as follows:     Let x=a + bi be a unit. Then there exists a y= c + di such that (a + bi)(c + di)=1.     This implies that ac - bd = 1 and ad + bc = 0 (call (1))     Now consider the identity (a^2 + b^2)(c^2 + d^2) = (ac - bd)^2 + (ad + bc)^2.     From (1) we have that (a^2 + b^2)(c^2 + d^2) = 1.     From this, it follows that a^2 + b^2 = 1, which implies that (a,b) = (+/-1,0) or (0,+/-1).     It follows then that x must be in the set (+1, -1, +i, -i).     Thus U(Z(i)) is a subset of (+1, -1, +i, -i). On the other hand, it can be easily checked that all the elements in (+1, -1, +i, -i) are also units. Hence (+1, -1, +i, -i) is subset of U(Z(i)).     Hence U(Z(i)) = (+1, -1, +i, -i). IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: tough number theory prob.   « Reply #10 on: Jun 12th, 2008, 12:04am » Quote Modify on Jun 11th, 2008, 11:12pm, LeoYard wrote: Now consider the identity (a^2 + b^2)(c^2 + d^2) = (ac - bd)^2 + (ad + bc)^2. This identity is precisely the multiplicative property of the norm on Z[i].  Considering the norm on Z[w] you should find a similar identity that will allow you to solve the problem. IP Logged LeoYard Newbie     Posts: 35 Re: tough number theory prob.   « Reply #11 on: Jun 12th, 2008, 11:37am » Quote Modify Thanx, i've just experienced a Eureka moment!     First I'll state the following property of norms:     If N is the norm on Z(w) then we have that the following property holds:     N(ab)= N(a)N(b)     Hence N(a + bw)N(c + dw) = N((a +bw)(c + dw)).     It follows that (a^2 - b^2 -b^(2)w)(c^2 -d^2 - d^(2)w) = (ac - bd)^2 - (-bd + ad + bc)^2 - (-bd + ad +bc)^2w     Now we know from before that ac - bd = 1 and that -bd + ad + bc = 0.     Thus we have that (a^2 - b^2 -b^(2)w)(c^2 -d^2 - d^(2)w) = 1.     However this implies that b = d = 0     This gives us a^2 * c^2 = 1.     It follows that a= +1 or -1.     Hence U(Z(w)) is in the set (+1, -1). However a quick check also shows that (+1, -1) is also in the set U(Z(w)).     Thus U(Z(w)) = (+1, -1). .................................................................... Does the property N(ab) = N(a)N(b) hold for any integral domain?     Furthermore is N(x) also a non-negative function over integral domains? IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: tough number theory prob.   « Reply #12 on: Jun 12th, 2008, 12:26pm » Quote Modify on Jun 12th, 2008, 11:37am, LeoYard wrote: Hence N(a + bw)N(c + dw) = N((a +bw)(c + dw)).     It follows that (a^2 - b^2 -b^(2)w)(c^2 -d^2 - d^(2)w) = (ac - bd)^2 - (-bd + ad + bc)^2 - (-bd + ad +bc)^2w I'm not sure where you got that formula from.  The conjugate of a+bw is a+bw2, so   N(a+bw) = (a+bw)(a+bw2)  = a2 + ab(w+w2) + b2w3  = a2 - ab + b2.   This leads to the identity (a2 - ab + b2)(c2 - cd + d2) = (ac-bd)2 - (ac-bd)(bc+ad-bd) + (bc+ad-bd)2.   However, this identity isn't really what's important.  What's important is the following: if xy=1, then N(x)N(y) = N(xy) = 1, and N(x), N(y) are integers when x,y Z[w] (or more generally, when they are algebraic integers, i.e., they satisfy monic polynomials with integer coefficients).  Furthermore, for imaginary quadratic number fields, the norm is positive definite, so there will only be finitely many possibilities for x, y.   Quote: Hence U(Z(w)) is in the set (+1, -1). You should find that the units are 1, w, and w2.   Quote: Does the property N(ab) = N(a)N(b) hold for any integral domain? The norm is not defined for an arbitrary integral domain.  But if you are working in a number field, then yes.  It follows from the formula you gave, since each embedding K -> C is multiplicative.   Quote: Furthermore is N(x) also a non-negative function over integral domains? No.  For one thing, N(-1) = (-1)[K:Q], so [K:Q] must be even.  But even in the case where K/Q is quadratic, it is only true for imaginary number fields.  E.g., N(a+bd) = a2 - d b2.  This takes on negative values iff d>0. IP Logged LeoYard Newbie     Posts: 35 Re: tough number theory prob.   « Reply #13 on: Jun 12th, 2008, 2:22pm » Quote Modify I thought it followed by definition that the conjugate of a + bw was a - bw. I guess its just the sign in front of the sqrt(-3) that changes, right? IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: tough number theory prob.   « Reply #14 on: Jun 12th, 2008, 3:14pm » Quote Modify Yes that's right.  Complex conjugation is the unique non-trivial automorphism of K = Q(w).  It sends (-3) to -(-3), and w to w2.  Alternatively, the minimal polynomial of w is x2+x+1=0, which has roots w and w2, so these two elements are conjugate. IP Logged LeoYard Newbie     Posts: 35 Re: tough number theory prob.   « Reply #15 on: Sep 27th, 2008, 5:05pm » Quote Modify I was on holidays, now I'm back to number theory.   How to prove that the following is an integral domain:     Z + Zk + Zk^2 where k is a root of the cubic equation k^3 - k^2 + 1 = 0.     The parts I'm having trouble with are the following:     (1) Proving that there are no zero divisors.   (2) Showing that it is closed under multiplication.   -------- If D is an integral domain then U(D) is an Abelian group with respect to multiplication (Theorem)   IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: tough number theory prob.   « Reply #16 on: Sep 27th, 2008, 7:52pm » Quote Modify To show that it is closed under multiplication, you will need to express k3 and k4 in terms of 1,k,k2.  The essential reason this works is that the polynomial x3-x2+1 is monic.   Now the short answer for why it is an integral domain is because it is a subring of a field.  I don't know if this makes sense to you, but in general, Z[x]/f(x) is a domain iff Q[x]/f(x) is a field iff f(x) is irreducible. « Last Edit: Sep 27th, 2008, 7:55pm by Eigenray » IP Logged LeoYard Newbie     Posts: 35 Re: tough number theory prob.   « Reply #17 on: Sep 29th, 2008, 1:12pm » Quote Modify on Sep 27th, 2008, 7:52pm, Eigenray wrote: To show that it is closed under multiplication, you will need to express k3 and k4 in terms of 1,k,k2.  The essential reason this works is that the polynomial x3-x2+1 is monic.   Now the short answer for why it is an integral domain is because it is a subring of a field.  I don't know if this makes sense to you, but in general, Z[x]/f(x) is a domain iff Q[x]/f(x) is a field iff f(x) is irreducible.   Thanks Eigenray.   I looked at  Z+Zi where i^2 + 1 = 0, first.   I'm studying Euclidean rings, however the rings we appear to be focused on in class are integral domains.   There is a theorem in my textbook which says the following:     Let m = 2,3 (mod 4) be a negative squarefree integer. Then Z + Zsqrt(m) is not a Euclidean domain for any integer m less than -7   Prove that Z + Zsqrt(m) is not even an Almost Euclidean domain.     How to show that there are no Almost Euclidean domains Z + Zsqrt(m) where m is squarefree and less than -7.     I haven't been able to prove the case when m = -7.     I got the feeling that Z + Zsqrt(-7) is a P.ID/Almost Euclidean since for many prime p such that (m/p) = 1, we have that p x^2 - my^2 for some integers x and y.     necessary condition for P.I.D's.,  but not be sufficient. IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: tough number theory prob.   « Reply #18 on: Sep 30th, 2008, 2:23am » Quote Modify What is an Almost Euclidean domain?  If you mean in the sense of Campoli it is equivalent to PID.   The ring [m] is a PID for m=-1,-2, but never for m < -2 square-free.  This is because I = (2, m+m) is not principal.  Suppose I = ().  Then | 2 implies N() | N(2) = 4, so N() = 1,2, or 4.  Check the following: If N()=1, then is a unit, but I is not the unit ideal.  N()=2 is impossible.  And N()=4 would imply that and 2 are associates, meaning I = (2), which is impossible.   However, when m=1 mod 4 (as -7 is), [m] is the wrong thing to look at.  Given a number field K, one should look at the ring of all algebraic integers of K: the elements of K which are roots of monic polynomials with integer coefficients.  If m=2,3 mod 4, then the only algebraic integers in (m) are a+bm, with a,b .  But if m=1 mod 4, then (1+m)/2 is an algebraic integer: it is a root of x2 - x + (1-m)/4.  So the correct ring to look at when m=1 mod 4 is [(1+m)/2] = { (a+bm)/2 | a,b integers of the same parity }.   For -m=3,7,11, [(1+m)/2] is a PID; in fact they are Euclidean with respect to the field norm.  For m=-15 (or any composite square-free negative m), this ring is not a PID.  For -m=19, 43, 67, 163, [(1+m)/2] is a PID which is not Euclidean.  It is a deep theorem that there are no other imaginary quadratic number fields for which the ring of integers is a PID. « Last Edit: Sep 30th, 2008, 2:38am by Eigenray » IP Logged LeoYard Newbie     Posts: 35 Re: tough number theory prob.   « Reply #19 on: Sep 30th, 2008, 1:39pm » Quote Modify Thanks Eigenray. Before I can answer directly to your post, I need to ask few questions to have this stuff clear in my mind.   A peripheral question:   When we say that a ring is never a PID because it is never integrally closed, does it mean that it isn't closed under multiplication?   There are general formulas for the class numbers of quadratic rings that can be used to check for the PID property   to be found at   http://mathworld.wolfram.com/ClassNumber.html   I'm interested to know how it is that the class number of a ring is suppose to be related to how well a ring is to being a unique factorization domain.   With regards to P.I.D's, I'm interested in which values of m we have that Z + Zsqrt(m) is P.I.D. I already know the answer to this when m is negative (except for m = -7), but I don't know the answer to this when m is a positive integer.   for m = 1 (mod 4) is the ring Z+Zsqrt(m) a PID?   do we know for which positive value m this ring is a PID?   is the ring Z+Z*((sqrt(m)+1)/2) is a PID for m=1 (mod 4)?   I went to "Class number problem" at http://en.wikipedia.org/wiki/Class_number_problem       IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: tough number theory prob.   « Reply #20 on: Oct 1st, 2008, 2:53am » Quote Modify on Sep 30th, 2008, 1:39pm, LeoYard wrote: When we say that a ring is never a PID because it is never integrally closed, does it mean that it isn't closed under multiplication? No.  For example, R=[m] is always closed under multiplication: (a+bm)(c+dm) = (ac+mbd)+(ad+bc)m.  But it is not integrally closed if m=1 mod 4 (and m is not a square).  The element x = (1+m)/2 of the field of fractions of R is integral over R, being a root of x2 - x + (1-m)/4 = 0, but it is not an element of R.   Since any PID is integrally closed (the rational roots theorem holds equally well over any PID), this means that R can't be a PID.  In fact, (2,1+m) isn't principal in R.  But over the larger ring S=[(1+m)/2], 1+m is divisible by 2, so (2,1+m) = (2) is principal in S.  But S may or may not be a PID.   Quote: I'm interested to know how it is that the class number of a ring is suppose to be related to how well a ring is to being a unique factorization domain. Well, it's related in the sense that h=1 iff R is a UFD.  A more accurate statement is that the class number tells you how close R is to being a PID: the class number tells you how many classes of ideals there are, where we say two ideals have the same class if they 'differ' by a principal ideal.   Another way of looking at it is that in the ring of integers of a number field, we have unique factorization of ideals.  What we would like, however, is unique factorization of elements.  Each element x gives an ideal (x), but not every ideal is of this form.  The class number measures the extent of this failure in a precise way.   For example, take R = [{-5}].  This has class number 2, with class group generated by the class of (2,1+{-5}).  So for any ideal I, exactly one of I and I*(2,1+{-5}) will be principal, so we can always find an element x such that either (x) = I or (x) = I*(2,1+{-5}).   If you know about modules there is another way of putting it.  Any ideal I of R is an R-module, and I 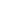R as R-modules iff I is principal.  More generally, if I ~ J in the class group of R, then J = xI for some x in the quotient field of K, and multiplication by x gives an R-module isomorphism from I to J.  Conversely, suppose I 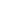J as R-modules.  Since the ideal classes form a group, there is an ideal I' such that I' I = (x) is principal.  Since I' I 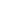I' J as R-modules, I' J is also principal, so J ~ I'-1 ~ I.  That is, two ideals of R are isomorphic as R-modules iff they are in the same ideal class, so the class group of R is also the set of isomorphism classes of ideals of R.   Quote: for m = 1 (mod 4) is the ring Z+Zsqrt(m) a PID? No, because it is not integrally closed (for m not a square).   Quote: do we know for which positive value m this ring is a PID?   is the ring Z+Z*((sqrt(m)+1)/2) is a PID for m=1 (mod 4)? Sometimes, but nobody knows whether they are PIDs infinitely often.  See A003172. « Last Edit: Oct 1st, 2008, 3:21am by Eigenray » IP Logged LeoYard Newbie     Posts: 35 Re: tough number theory prob.   « Reply #21 on: Oct 1st, 2008, 1:59pm » Quote Modify Question: is the ring Z+Z*((sqrt(m)+1)/2) is a PID for m=1 (mod 4)?     You said: Sometimes, but nobody knows whether they are PIDs infinitely often   My new question:  is this an unsolved problem for even when m is negative? IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: tough number theory prob.   « Reply #22 on: Oct 1st, 2008, 3:15pm » Quote Modify For m=1 mod 4, m < 0, [(1+m)/2] is a PID only for -m = 3,7,11,19,43,67,163.  In addition to [i] and [{-2}], these are the only rings of integers of imaginary quadratic number fields to be PIDs, as you can see on the class number problem page. IP Logged Benny Uberpuzzler     Gender: Posts: 1024 Re: tough number theory prob.   « Reply #23 on: Oct 17th, 2008, 4:15pm » Quote Modify Interesting discussions going on here!   Why isn't the remainder symbol "rem" being used? I heard it being used in some lectures, but I couldn't find in textbooks.   Say we have the set {..., -1, +2, +5, +8, +11, +14, ...} These numbers all leave a remainder of 2 when divided by 3. We write: rem(5,3) = rem(8,3) = rem(11,3) =... = 2   If a = b (mod n) would that mean:   a = (rem(a,n)) (mod n) a = b (mod n) iff (rem(a,n)) = (rem(b,n)) IP Logged If we want to understand our world — or how to change it — we must first understand the rational choices that shape it. Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: tough number theory prob.   « Reply #24 on: Oct 18th, 2008, 8:22am » Quote Modify Probably because it's not very convenient.   It's a slight abuse of notation to say that "a = b (mod n)", because while "b mod n" is well-defined (it is the image of b in the quotient /n or the set of elements of congruent to b modulo n), it is not really equal to a.  So more technically correct notation would be "a (b mod n)", or "(a mod n) = (b mod n)".  But it is easier to just write "a = b", and then write "mod n" at the end to mean that we are modifying what it means to be equal.   So really it defines a new relation n where a n b iff a and b are congruent modulo n.  When n is understood this is usually just written .  Of course this notation is used much more generally, if we want to mod out a group by a subgroup, a module by a submodule, a space by a group action, etc.  One can also draw bars over a and b to denote elements of the quotient, and write a-bar = b-bar, or use brackets: [a] = [b], when one is thinking of equivalence classes. IP Logged Pages: 1 2  Reply Notify of replies Send Topic Print Forum Jump: ----------------------------- riddles -----------------------------  - easy   - medium   - hard   - what am i   - what happened   - microsoft   - cs => putnam exam (pure math)   - suggestions, help, and FAQ   - general problem-solving / chatting / whatever ----------------------------- general -----------------------------  - guestbook   - truth   - complex analysis   - wanted   - psychology   - chinese « Previous topic | Next topic »

Powered by YaBB 1 Gold - SP 1.4!
Forum software copyright © 2000-2004 Yet another Bulletin Board