Author |
Topic: Abelian Groups? (Read 919 times) |
|
Barukh
Uberpuzzler
Gender: 
Posts: 2276
|
 |
Abelian Groups?
« on: Oct 23rd, 2003, 2:59am » |
 Quote  Modify
|
1. Prove that any group in which every element x satisfies x2 = 1 is abelian.
2. What if x3 = 1 for every x?
|
|
 IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Abelian Groups?
« Reply #1 on: Oct 23rd, 2003, 3:39am » |
Quote Modify
|
If, like me, you're wondering what the ** Abelian groups are, go to http://mathworld.wolfram.com/AbelianGroup.html
in short:
"A group for which the elements commute (i.e., AB = BA for all elements A and B) is called an Abelian group."
Something else crucial I didn't know:
"A group G is a finite or infinite set of elements together with a binary operation which together satisfy the four fundamental properties of closure, associativity, the identity property, and the inverse property. "
|
| « Last Edit: Oct 23rd, 2003, 4:08am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Abelian Groups?
« Reply #2 on: Oct 23rd, 2003, 4:28am » |
Quote Modify
|
I think I have 1)..
::
using random elements x and y from any group G satisfying forall x in G: xx=1
(xy)(xy) = 1
((xy)x)y = 1
((xy)x)yy = y
(xy)x = y
(xy)xx = yx
xy=yx, so for all x,y: xy=yx, and thus the group is Abelian.
::
|
| « Last Edit: Oct 23rd, 2003, 5:06am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Abelian Groups?
« Reply #3 on: Oct 23rd, 2003, 5:58am » |
Quote Modify
|
Good work, towr! Besides, I am glad you've learned some new stuff.
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Abelian Groups?
« Reply #4 on: Oct 23rd, 2003, 6:05am » |
Quote Modify
|
on Oct 23rd, 2003, 5:58am, Barukh wrote:| Besides, I am glad you've learned some new stuff. |
|
Yes, me too. I mean, that's what puzzles are for really, aren't they..
on the second question :: I'd guess no, but I don't know how to proof it.. Perhaps find a group for which it doesn't work?::
|
| « Last Edit: Oct 23rd, 2003, 6:05am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
wowbagger
Uberpuzzler
 
Gender:
Posts: 727
|
|
Re: Abelian Groups?
« Reply #5 on: Oct 23rd, 2003, 6:08am » |
Quote Modify
|
Funny what basic things these really clever people don't know... 
Not sure whether that's what you're after, Barukh, but in case 2.:
(xy)(xy)(xy) = 1 leads to
(xy)(xy) = (yy)(xx) which means that
(xy)-1 = y-1x-1 = (yy)(xx)
.
|
|
IP Logged |
"You're a jerk, <your surname>!"
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Abelian Groups?
« Reply #6 on: Oct 23rd, 2003, 7:59am » |
Quote Modify
|
on Oct 23rd, 2003, 6:05am, towr wrote:| on the second question :: |
|
towr, your guess is right, as is the way to proof. However, it's not trivial, so here's a hint: one of the possible groups has matrices as elements
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Abelian Groups?
« Reply #7 on: Oct 23rd, 2003, 8:02am » |
Quote Modify
|
on Oct 23rd, 2003, 6:08am, wowbagger wrote:| Not sure whether that's what you're after, Barukh, but in case 2.: |
|
wowbagger, your derivation is correct; however, how does it settle the question if the group is abelian?
|
|
IP Logged |
|
|
|
wowbagger
Uberpuzzler
Gender:
Posts: 727
|
|
Re: Abelian Groups?
« Reply #8 on: Oct 23rd, 2003, 8:11am » |
Quote Modify
|
on Oct 23rd, 2003, 8:02am, Barukh wrote:| how does it settle the question if the group is abelian? |
|
Heh, it doesn't. As I said, I wasn't sure what you expected. It seems that the question from the first part carries over to the second. Anyway, it's nice to fiddle about with this stuff every once in a while, even though my "result" is probably not very interesting.
I was never really good at finding counter-examples.
|
|
IP Logged |
"You're a jerk, <your surname>!"
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Abelian Groups?
« Reply #9 on: Oct 25th, 2003, 7:49am » |
Quote Modify
|
on Oct 24th, 2003, 10:44pm, Pietro K.C. wrote:How about ...
It's late. Is anything wrong with the above? |
|
Pietro, I'm afraid, G is not a group: not every composition of 2 rotations is again a rotation in the group. Or maybe, I didn't understand the definition of the group.
Here's a counter-example I'm familiar with: Take a group G of 3x3 matrices of the form:
1 a b0 1 c0 0 1where a, b, c are numbers 0, 1, 2, and the operation is ordinary matrix multiplication modulo 3. Simple manipulations reveal that G is not commutative, and every matrix in G raised to power 3 gives the identity matrix.
G consists of 27 elements (in group theory: has order 27). I have also seen another counter-example with the group of order 27. I am curious: is there a counter-example of order less than 27?
|
|
IP Logged |
|
|
|
Pietro K.C.
Full Member
Gender:
Posts: 213
|
|
Re: Abelian Groups?
« Reply #10 on: Oct 27th, 2003, 6:01pm » |
Quote Modify
|
Right you are. Duh.
I meant to define G as all possible compositions of such rotations (like defining a vector space by giving a basis and taking all linear combinations of its elements), but alas, I only "showed" x3 = 1 for the "basis" elements.
Before it got late and I posted all that nonsense, I tried to conjure up a counter-example involving matrices, which are non-commutative par excellence, but the calculations started to get a little too messy.
I thought your final question was very interesting. For all elements, x3 = 1, and the smallest non-abelian group you know of has order 33... maybe there's something there?
So here's a follow-up: find, with proof, the non-abelian group of smallest order that satisfies [forall]x[in]G : x3 = 1.
|
|
IP Logged |
"I always wondered about the meaning of life. So I looked it up in the dictionary under 'L' and there it was --- the meaning of life. It was not what I expected." (Dogbert)
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Abelian Groups?
« Reply #11 on: Nov 10th, 2003, 5:10pm » |
Quote Modify
|
on Oct 23rd, 2003, 7:59am, Barukh wrote:| However, it's not trivial, so here's a hint: one of the possible groups has matrices as elements. |
|
I know the question has been answered, but I would like to point out that this is not much of a hint!
All finite groups can be expressed as a group of matrices, as can all Lie groups (groups with "manifold" structure - i.e. locally they look like [bbr]n in a differentiable fashion, where n is finite).
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Abelian Groups?
« Reply #12 on: Nov 11th, 2003, 12:42am » |
Quote Modify
|
It may not be much of a hint to you, but it is to some of us. It implies there's a relatively small set of small matrices which do the trick. That helps limit the search space of all possible groups a lot
I was allready trying matrices though, but those were 2x2 matrices which didn't work out..
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Abelian Groups?
« Reply #13 on: Nov 11th, 2003, 2:18am » |
Quote Modify
|
towr, your last reply was a relief for me 
|
|
IP Logged |
|
|
|
ecoist
Senior Riddler
Gender:
Posts: 405
|
|
Re: Abelian Groups?
« Reply #14 on: Dec 28th, 2006, 9:26pm » |
Quote Modify
|
Barukh asked if there is an example of order less than 27. The answer is no. Since every element is of order 1 or 3, the group is a finite 3-group. All p-groups of order p2, where p is a prime, are abelian.
Another way to look at a counterexample is to note that GL(2,Z3) contains a matrix of order three. This matrix and Z32 form a semi-direct product of Z3xZ3 by an automorphism of order 3.
|
|
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Abelian Groups?
« Reply #15 on: Dec 29th, 2006, 12:59am » |
Quote Modify
|
Suppose that G is a finite group. If more than 3/4 of the elements x satisfy x2=1, show that G is abelian.
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Abelian Groups?
« Reply #16 on: Dec 30th, 2006, 5:24am » |
Quote Modify
|
Let I 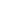 G be the set of elements satisfying x2 = 1. Take s  I, and consider the set I(s) = I  sI. Since |sI| = |I| > 3/4 |G|, |I(s)| > |G|/2.
Now, for every r I(s), we have r = st, t I. Thus, r = s-1t-1. But r = r-1 = t-1s-1 = ts, therefore s commutes with t. Because r was chosen arbitrarily, there are at least |I(s)| > |G|/2 elements commuting with s. Therefore, C(s) – the centralizer of s - is the whole G.
As s was also chosen arbitrarily, we get in the same way, C(I) = G. It means for every g G, at least |I| > |G|/2 elements commute with g. Therefore, C(G) = G.
|
|
IP Logged |
|
|
|
ecoist
Senior Riddler
Gender:
Posts: 405
|
|
Re: Abelian Groups?
« Reply #17 on: Dec 30th, 2006, 11:14am » |
Quote Modify
|
Nice, Barukh! It appears that the three quarters condition is best possible because the direct product of an elementary abelian 2-group with the dihedral group of order 8 has exactly three quarters of its elements satisfying the equation x2=1.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print