Beginning in 1945, with the work of William K. Estes (published with B.F. Skinner, who was his graduate advisor), a number of psychologists began to employ mathematical models as a medium for writing psychological theories of learning and memory. Later, the development of the high-speed computer, not to mention the computer model of the mind, led to the addition of computational models to the theorist's armamentarium. I am neither a mathematical psychologist nor a computer modeler, so my treatment of these topics will be necessarily brief, unsophisticated, and highly selective. But I do have to say something about this aspect of learning and memory, so here goes.
In his retirement lecture (2012), UCB's Prof. Tom Wickens has listed the three postulates of most mathematical models in psychology:
Wickens noted that mathematical models "represents process in a way that abstracts the most important elements and allows you to see their implications. Because it needs to be explicit, you can (and should, although many people slough over it) make a list of its assumptions. Often listing the assumptions forces one to clarify a fuzzier verbal formulation or identifies where it is not determinant. He went on to give some examples:
He also pointed out two "sins" of mathematical modeling:
The mathematical modeling of psychological processes has its roots in classical psychophysics -- Weber's, Fechner's, and Stevens' laws and the like.
So far as learning and memory is concerned, mathematical modeling has its origins in the systematic behavior theory of Clark H. Hull, as expressed in the postulates of his Principles of Behavior (1943) and his A Behavior System (1952). The final version of Hull's system contained a set of formal definitions, theorems, and proofs, and a series of 17 postulates and 17 corollaries.
For Hull, a conditioned stimulus arouses one or more responses stored in memory, each of which has both an excitatory habit strength (H), as well as an inhibitory strength (SIR). There is also a general inhibitory factor, such as mere fatigue (IR). So, the net strength of a response, E, is given by the following formula:
While this looks like the usual social-scientific pseudomathematics, in fact Hull intended his system to be rigorously quantitative, so that various elements in his equations could be given precise numerical values, and the equations themselves could generate precise quantitative predictions about behavior in new experimental situations.
As with psychophysics, just the attempt to write a psychological theory in the language of mathematical formulas was a landmark in the evolution of psychology as a science. At the same time, Hull's efforts at mathematical precision led to his downfall, because it turned out that his formulas made the wrong predictions. In a famous Psychological Review paper, for example, Gleitman, Nachmias, and Neisser showed that, according to Hull, reinforced conditioning trials would ultimately lead to the extinction of the conditioned response. This is because (when you look at the formulas in detail) there is an asymptote on excitatory habit strength -- at some point, reinforcement no longer increases habit strength. But because there is no limit on inhibition (again, when you look at the formulas in detail), eventually response strength will decline to baseline. This paradox, that continued reinforcement will actually lead to a decrement in response, not to mention inhibition of response below zero, effectively killed Hull's system.
Gleitman et al. had originally planned their paper as the first salvo in a series of papers intended to dismantle Hullian theory, but no further critique was necessary. although a large number of neo-Hullian theorists continued to work in the tradition of Hullian learning theory -- among them, Neal Miller, Hobart Mowrer, Kenneth Spence, Abram Amsel, and Frank Logan. The general idea that behavior is set in motion by motivational states (Drive), and that reinforcement works by virtue of drive-reduction, is the hallmark of Hullian and neo-Hullian learning theory.
But in the present context, the important point is that that Hull specified his theory with sufficient mathematical precision that predictions could be derived from it that could be empirically tested. That his theory failed the test is of secondary importance.
For a overview of Hull's system, see any of the editions of Hilgard's Theories of Learning. This summary is derived from the 2nd edition (1956). See also Hilgard's Psychology in America: A Historical Survey (1987).
Hull's theory was a theory of learning, not memory, and animal learning at that. And because it focused on drive and reinforcement, it wasn't an especially cognitive theory, either. An explicitly cognitive theory of human learning and memory, developed by William K. Estes, is known as stimulus-sampling theory. Somewhat paradoxically, stimulus-sampling theory had its origins in the animal-learning laboratory; and even more paradoxically, it had its origins in the laboratory of B.F. Skinner, who was Estes' graduate-school mentor at the University of Minnesota. Together, Estes and Skinner did important work on the effects of punishment. A paper by Estes and Skinner (1941) on conditioned fear and anxiety is one of the few times that Skinner, a radical behaviorist, ever allowed himself to refer to an organism's internal mental state! Skinner took Estes with him when he left Minnesota for Indiana. And later, Estes took a position at Harvard, where he and Skinner were again colleagues (Skinner in retirement). By that time, however, Estes had left animal learning entirely, and was focused exclusively on human learning and memory. along with R. Duncan Luce, Estes was one of the founders of mathematical psychology. For their contributions, they both were awarded the National Medal of Science.
Prior to Estes, mathematical psychology mostly took the form of curve-fitting exercises in which performance (e.g., % correct) was plotted against practice. (e.g., time or trials).
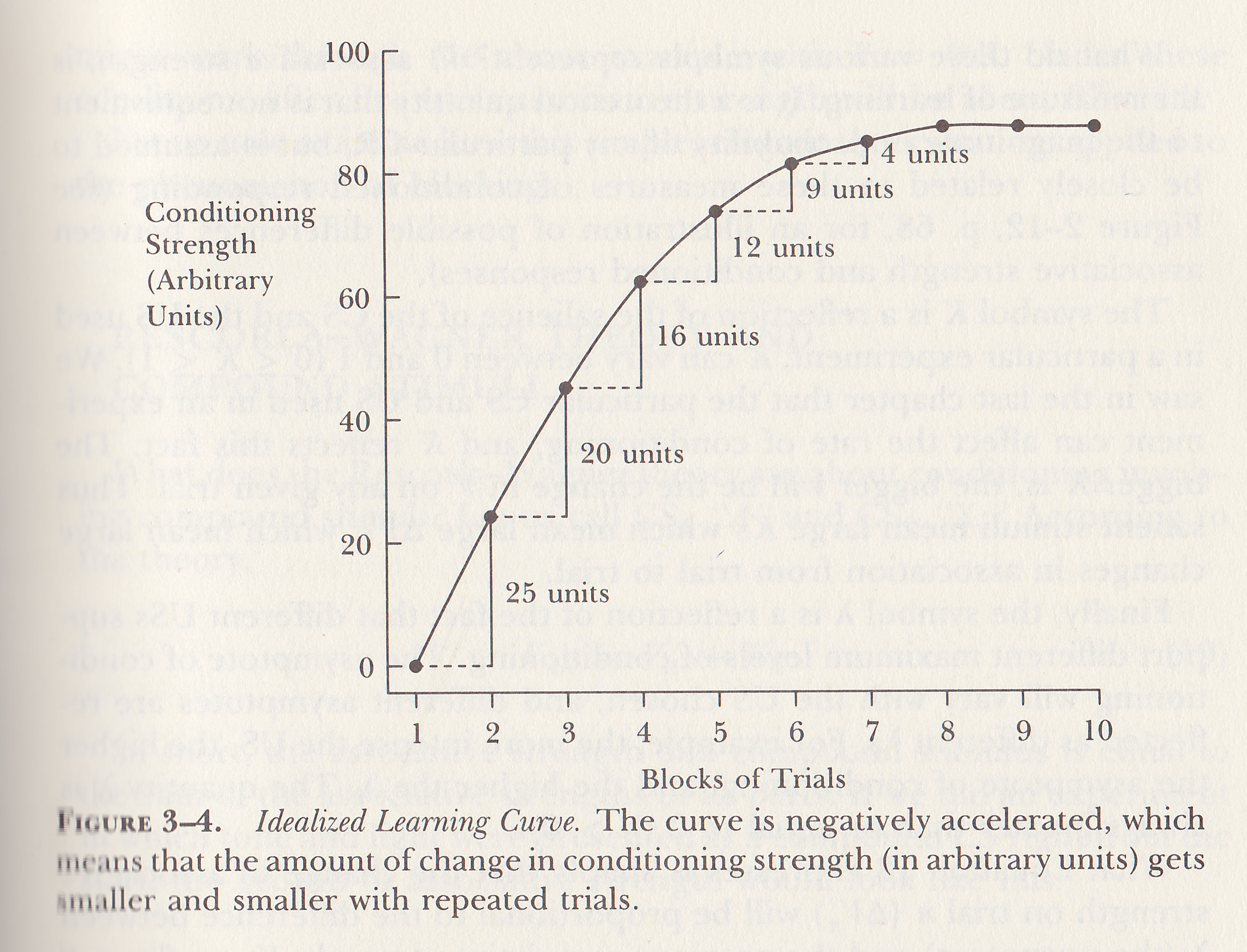 such a
method, Hull et al. (1940) observed that the learning
curve was characterized by negative acceleration:
large initial gains followed by smaller gains as learning
approached asymptote. Put another way, the gain in
learning on each trial was a constant fraction of the
amount remaining to be learned. This is the idealized learning
curve.
such a
method, Hull et al. (1940) observed that the learning
curve was characterized by negative acceleration:
large initial gains followed by smaller gains as learning
approached asymptote. Put another way, the gain in
learning on each trial was a constant fraction of the
amount remaining to be learned. This is the idealized learning
curve.
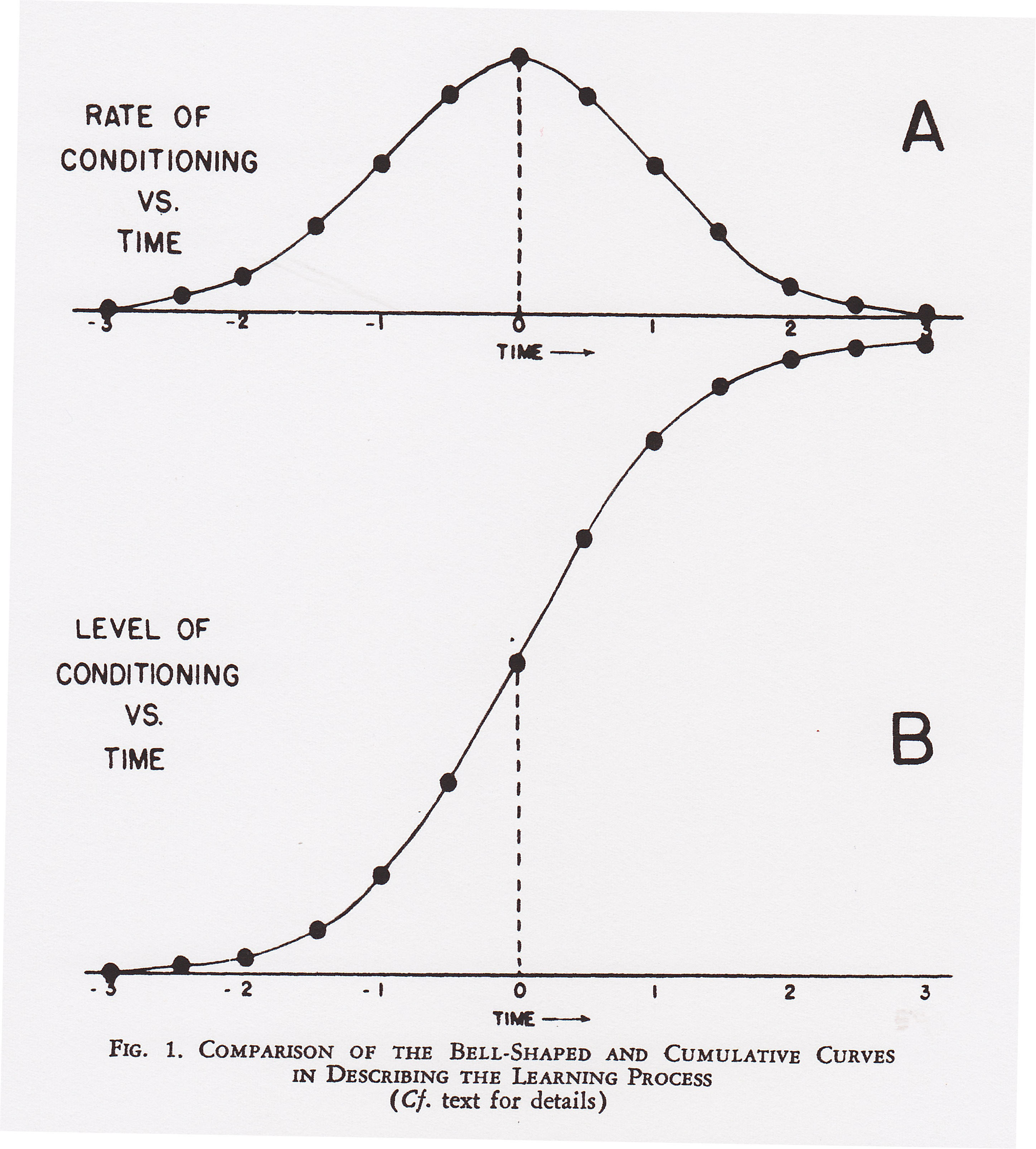 and Girden
(1951), however, examining actual, empirical
learning curves derived from a wide variety of experiments
(and species), determined that the learning curve is,
initially, positively accelerated, yielding an "ogival",
"sigmoidal", or simply "S-shaped" learning
curve: initial slow growth followed by rapid acceleration,
then a marked change in slope, leading to an asymptote. This
is the classic learning curve.
and Girden
(1951), however, examining actual, empirical
learning curves derived from a wide variety of experiments
(and species), determined that the learning curve is,
initially, positively accelerated, yielding an "ogival",
"sigmoidal", or simply "S-shaped" learning
curve: initial slow growth followed by rapid acceleration,
then a marked change in slope, leading to an asymptote. This
is the classic learning curve.Estes viewed such attempts as purely empirical (you get a series of points, and find the curve that best fits them), and lacking a rational basis. Based on a theory of one-trial learning proposed by Edwin R. Guthrie (1930, 1935): in any situation, an organism tends to do what it did the last time it was in that situation. But, of course, the organism is rarely in precisely the same situation. Guthrie proposed that each learning trial created a separate stimulus-response habit, each acquired in a single trial. The appearance of gradual improvement, as reflected in the typical learning curve, is caused by the gradual accumulation of connections between many different stimuli and many different response movements.
To take an example from Hilgard and Bower (1981), of learning to shoot baskets in basketball. A player throws the ball from one part of the court, from a particular posture, and either hits the basket or he doesn't. If he does hit the basket, he has learned, in that one trial, to hit the basket from that particular position. The next time, he shoots from a slightly different part of the court, or from a slightly different posture, and he tosses the ball slightly differently. If he hits the basket, he has learned that particular stimulus-response connection. A player acquires basketball skill through the cumulative attachment of many slightly different response movements to many different stimulus situations. To borrow a phrase that Guthrie used somewhere (I'm sure I got this from Hilgard), what the subject is doing is learning to shoot baskets; but this skill reflects a number of discrete learning experiences, each consisting of a single trial of learning.
One-trial learning is not as strange as it might initially seem.
In a verbal-learning experiment, we usually think of a memory trace being strengthened across learning trials, but Endel Tulving once gave the following demonstration of one-trial learning. He spoke a single word, e.g. (I forget what the word was, and it doesn't matter), assassin, to a subject, and then asked the subject what he had just said. The subject replied "assassin", at which point Tulving turned to his audience and said: "See, learning occurs in just a single trial). What Tulving meant was that episodic memory was memory for an event that occupied a unique position and time and space. There can only be one such event. Therefore, episodic memories must be acquired, encoded, in a single trial. What causes forgetting is not poor encoding, but poor retrieval.
In a classic experiment, Rock (1957) employed a paired-associate learning procedure in which any pair not correctly recalled on a particular trial was replaced by another pair; if the second pair was not recalled, it was replaced by yet a third pair, and so on. Rock found that it took no longer to learn such a list than to learn a standard list, in which the same pairs were presented on each trial until the subject recalled them all correctly.
Traditional memory theories generally follow Ebbinghaus's Law of Repetition (and Thorndike's Law of Practice) in assuming that a memory trace, like a stimulus-response association, is strengthened by repetition over time. But Douglas Hintzman (1976) argued that each repetition produces a separate memory trace, and that what appears to be increasing memory strength over learning trials really reflects an increasing pool of episodic traces. He built a computer simulation of memory, known as MINERVA 2, on this principle. MINERVA 2 successfully simulates the performance of real subjects on a variety of memory tasks, and I'll have more to say about it later.
A similar multiple trace theory has been proposed by Nadel and Moscovich (1997) to explain the occurrence of retrograde amnesia in patients with the amnesic syndrome. Damage to the hippocampus and other portions of the medial temporal lobe can easily explain anterograde amnesia. But why should hippocampal damage impair access to memories that had been encoded long before the damage occurred? Some theorists, propose that hippocampal damage interferes with consolidation; because consolidation takes a long time, hippocampal damage can disrupt the consolidation process for memories whose consolidation began long before the damage, thus resulting in an apparent retrograde amnesia. It's not a very satisfying explanation -- pretty post-hoc, if you ask me. Instead, Nadel and Moscovich argue that every retrieval ("reactivation") of a memory creates a new trace of that episode. Retrieval is facilitated by the existence of these multiple memory traces. But by virtue of hippocampal damage, these new traces are poorly encoded. In this way, the amnesic patient loses accesses to "old" memories as well as new ones.
But back to Estes' stimulus-sampling theory.
Following Guthrie, Estes
proposed that there was a large number of stimuli available to
be conditioned to any particular response. On a particular
trial, only a sample of these stimuli become associated with
the response. On each trial, an overlapping sample of stimuli
(some old, some new) are conditioned to the response, with the
result that, on each successive trial, fewer and fewer new
stimuli would be so conditioned. This results in a learning
curve that rises over trials, but with decreasing gains on
each trial. The An early (1951) "large-element" version of the
model assumed that the sampling process involved many
conditioned stimuli; later versions (e.g., 1959) involved only
a few stimuli, or even of just one random stimulus element.
From assumptions like these, Estes derived a set of learning equations that predict the probability of a correct response on any particular trial, and thus account for the acquisition and extinction of conditioned responses. Rather than fitting curves to empirical data, Estes showed that empirical data fit curves generated by his equations.
Although this presentation has used a "stimulus-response" language familiar from animal learning experiments, Estes caught on to the cognitive revolution quite early. For example, he assumes that what the organism learns are actually internal representations of stimuli, responses, and outcomes (reinforcements). To take another example, stimulus sampling is a product of attention and the organism's internal motivational state. Estes easily made the shift from classical and instrumental conditioning to human cognition, applying various forms of stimulus-sampling theory to problems of verbal learning, concept formation, and recognition memory. Getting about as far from his Skinnerian origins as anyone could get Estes (1972, 1973) abandoned the behaviorist view that learning is a matter of connecting stimuli to responses, and instead focused on learning as the storage and retrieval of memories for sequences of events.
For a overview of Estes' system, see the 5th edition of Hilgard's Theories of Learning, co-authored with Gordon H. Bower (whose earliest work was also in the animal-learning laboratory, under the Hullian Frank Logan), from which this summary is derived. See also Hilgard's Psychology in America: A Historical Survey (1987).
The Evolution of Interactive Models of Processing
 Across
the
100 years from Donders (1868-1869) to Sternberg (1969), models
of human cognition have generally assumed what McClelland
(1979) called the discrete stage model of information
processing. That is, information is assumed to be
processed in discrete stages, and information is passed from
one stage to the next
Across
the
100 years from Donders (1868-1869) to Sternberg (1969), models
of human cognition have generally assumed what McClelland
(1979) called the discrete stage model of information
processing. That is, information is assumed to be
processed in discrete stages, and information is passed from
one stage to the next
. It was further assumed that processing at one stage
had to be completed before processing at the next stage could
begin. Note that processing is assumed to proceed in
only one direction, from "bottom up".
These two assumptions, of serial independence, took cognitive psychology a long way, but eventually the assumptions were challenged by experimental data.
Of particular interest (at least to me), is the word-letter phenomenon, also known as the word superiority effect (Johnston & McClelland, 1973, 1974). Consider the process of reading a written word. According to the discrete stage model, reading happens something like this:
 It turns out
though, that subjects who are asked to detect a letter in a
string of letters do so more quickly when that letter string
comprises a familiar word, as opposed to a non-word (this is
the word-letter phenomenon). In a variant on
this procedure, subjects are asked to decide whether a briefly
presented stimulus is a particular word or letter: it turns
out that subjects find it easier to decide whether the word
was coin or join than to decide whether a
string included the letter J or C. This
presented a puzzle because, logically, the word join
includes the letter J and the word coin
includes the letter C. So if you have identified
the word as coin, then you've already identified its
first letter as C.
It turns out
though, that subjects who are asked to detect a letter in a
string of letters do so more quickly when that letter string
comprises a familiar word, as opposed to a non-word (this is
the word-letter phenomenon). In a variant on
this procedure, subjects are asked to decide whether a briefly
presented stimulus is a particular word or letter: it turns
out that subjects find it easier to decide whether the word
was coin or join than to decide whether a
string included the letter J or C. This
presented a puzzle because, logically, the word join
includes the letter J and the word coin
includes the letter C. So if you have identified
the word as coin, then you've already identified its
first letter as C.
 In
In ![]() order to
accommodate results such as these, McClelland (1979) proposed
a cascade model of human information processing.
The cascade model retains the assumption that information
processing occurs in stages, but it abandons the assumption
that processing at one stage is completed before processing at
the next stage can begin. Each stage operates
continuously, passing information to the next stage even
before its work has been concluded. In the context of
the word-letter phenomenon, this means that, provided that
enough of the right kind of information is included in the
cascade, identification can be completed at the word level
before it is completed at the letter level.
order to
accommodate results such as these, McClelland (1979) proposed
a cascade model of human information processing.
The cascade model retains the assumption that information
processing occurs in stages, but it abandons the assumption
that processing at one stage is completed before processing at
the next stage can begin. Each stage operates
continuously, passing information to the next stage even
before its work has been concluded. In the context of
the word-letter phenomenon, this means that, provided that
enough of the right kind of information is included in the
cascade, identification can be completed at the word level
before it is completed at the letter level.
 Still,
on
average, it ought to be easier to identify a single letter
than an entire word. But there are a number of instances
where, for example, our knowledge of what we might be
perceiving influences how we process stimulus inputs. A
classic example, noted by Rumelhart (1977), is reading.
McClelland and Rumelhart (1981) listed a number of other
instances, including the word superiority effect and the
word-letter phenomenon -- all of which indicate that knowledge
and expectations concerning context influence the processing
of a stimulus. Accordingly, a better explanation is
offered by a model that abandons seriality in favor of
bidirectionality, and also permits processing at a "later",
more complex stage to affect processing at an "earlier",
simpler one. In other words, the passing of information
needs to be bidirectional, involving both bottom-up
and top-down processing.
Still,
on
average, it ought to be easier to identify a single letter
than an entire word. But there are a number of instances
where, for example, our knowledge of what we might be
perceiving influences how we process stimulus inputs. A
classic example, noted by Rumelhart (1977), is reading.
McClelland and Rumelhart (1981) listed a number of other
instances, including the word superiority effect and the
word-letter phenomenon -- all of which indicate that knowledge
and expectations concerning context influence the processing
of a stimulus. Accordingly, a better explanation is
offered by a model that abandons seriality in favor of
bidirectionality, and also permits processing at a "later",
more complex stage to affect processing at an "earlier",
simpler one. In other words, the passing of information
needs to be bidirectional, involving both bottom-up
and top-down processing.
Such a model of interactive activation was offered by McClelland and Rumelhart (1981; Rumelhart & McClelland, 1982).
In their 1981 and 1982 papers, McClelland and Rumelhart assumed that features, letters and words were represented by discrete nodes in an associative network -- the interactive activation model described above is, technically, a "localist" model as described in the lectures on Knowledge Representation. Later, they switched from this localist representation to a distributed representation, in which knowledge of individual features, letters, and words is represented as a pattern of activation distributed widely across the network. Thus was born the idea of parallel distributed processing, announced in a trio of edited volumes published in 1986. These publications initiated the connectionist revolution in analyses of human cognition foreshadowed by D.O. Hebb's idea of cell assemblies. You'll find more information on connectionist models in the lectures on Knowledge Representation.
There is a little irony here:
the sample connectionist simulations supplied with the PDP
books run on Apple or Microsoft operating systems, meaning
they employ an architecture that is both locationist and
serial! But never mind.
Connectionist models gradually
evolved into the "Large Language" architectures for ChatGPT
and similar Artificial Intelligence (AI) systems that began to
emerge in the 2020s. This story is effectively told in
"Metamorphosis", a profile of Geoffrey Hinton, often called
"the godfather of AI), by Joshua Rothman (New Yorker, 11/20/2023).
Highly recommended.
Do We Need Multiple Memory Systems?
Combining Computational Modeling with
Behavioral and Neuroscientific Analyses
By any standard, acquisition views such as transfer-appropriate processing and process dissociation are more popular than the activation view as an alternative to the multiple-systems view of implicit memory. However, Dorfman's research strongly suggests that there is still life in the activation view. What about the multiple-systems view? As even some processing theorists concede, the processing view has difficulty accounting for implicit memory in amnesic patients; and in fact, the most vigorous proponents of the multiple-systems view have been those theorists who have studied dissociations between explicit and implicit memory in brain-damaged patients, where the role of different brain systems stands out in bold relief. Moreover, the memory-systems view can incorporate the processing view, by the simple assumption that certain brain systems perform perceptual processing, while other brain systems perform conceptual processing. So now it is important to confront the memory-systems view directly: are multiple memory systems necessary to account for dissociations between explicit and implicit memory in amnesic patients?
A negative answer to this question comes from an investigative approach to memory and cognition that is often ignored by neuroscientists: the mathematical and computational modeling of memory and other cognitive processes. Over the past several decades, a great deal of progress has been made in developing operating computer simulations that are, essentially, formal theories of how human memory works. Among these are the various versions, known in the memory trade by their acronyms, of ACT, SAM, MINERVA2, and TODAM. Although these models have many differences among them, one feature they hold in common is the assumption that there is only one memory storage system, which various processes operating within it. The question, then, is whether these computational models can show the same sorts of dissociations between explicit memory seen in the actual performance of amnesic patients. If so, then it would not be necessary to postulate multiple memory systems in order to account for preserved implicit memory in amnesia.
To understand where this is coming from, and where this is going, it's important to understand an important feature of some neuroscientific approaches to the study of memory (and of cognition in general, and indeed all of mental life). This feature is what I have called the rhetoric of constraint (Kihlstrom, 2010).
The rhetoric of constraint was brought
from cognitive neuroscience into the emerging social
neuroscience.
All I want to say here is that it just
isn't true. Psychological theory -- that is, theory
concerning mental structures and processes -- is not
constrained by biological evidence concerning neural
structures and processes. In fact, the situation is
quite the reverse: proper interpretation of biological
function requires a valid psychological theory of mental
structure and function. To take an example from the
domain of memory, interpretation of hippocampal function has
changed as psychological theories of memory have
evolved. Psychology constrains neuroscience, not the
reverse. Nothing about the biological structure and
function of the hippocampus plays any role in a psychological
theory of memory.
A softer version of the neuroscientific
approach simply argues that evidence of three different kinds
converges on our understanding of a psychological topic such
as memory.
This method of converging strategies doesn't imply that neuroscientific evidence can constrain psychological theory. Instead, it asserts, quite reasonably, that neuroscientific evidence can answer a question of relevance to psychologists -- what are the neural substrates of mental life? The cognitive neuroscience approach is, obviously, the only approach to answering that question. But, to repeat, answering that question assumes that we already know what the nature of mental life is.
As an example of converging strategies,
consider the question of multiple memory systems.
Traditionally, psychological theories of memory were based on
what might be called a unistore model of memory --
that is, the idea that memory consists of a single, unitary
storage structure.
Of course, we have long known of exceptions
to the unistore view.
Neuroscientific evidence for multiple memory systems comes mostly from studies of the amnesic syndrome in patients with damage in the medial temporal lobe (including the hippocampus) or the diencephalon (including the mammillary bodies).
A study by Knowlton and Squire (1993) on learning in amnesia employed a set of dot patterns. Each of these patterns was a variant on a prototype, or average, portrayed on the right-hand side. An earlier study by Posner and Keele, who developed the patterns in the first place, found that subjects who studied the dot-pattern variants falsely recognized the prototype as having been presented as well. They also falsely recognized other variants on the prototypical pattern, especially if the test items were low distortions of the prototype. Subjects were less likely to falsely recognize high distortions from the prototype, and they rarely falsely recognized random dot patterns that bore no relation to the prototype. Posner and Keele concluded from their study that people abstracted a "schema" representing the gist of related experiences, and that this summary concept was then used to guide later memory judgments.
The overall pattern of performance, of course, is a dissociation between recognition and categorization. The amnesic patients were able to acquire knowledge of a novel category from exposure to exemplars of that category, even though they did not remember the exemplars to which they had been exposed. This is a variant on source amnesia, in which subjects acquire new semantic or procedural knowledge, but forget the episodic source of that knowledge.
Knowlton and Squire went further, though, to invoke multiple memory systems. In their view, amnesics suffer damage to particular areas, like the medial temporal lobe memory system, that impairs recognition performance but spares categorization performance. Therefore, they concluded, categorization is mot mediated by the medial temporal lobe memory system, but rather by some other dedicated brain system. The implication is that categorization is mediated by the same, separate, cortical system that mediates implicit memory, implicit learning, and other forms of what Squire prefers to call "non-declarative" memory. Thus, Knowlton and Squire's study appeared to provide evidence for the existence of two separate and independent brain systems, one mediating explicit episodic memory, and the other mediating implicit memory and implicit learning.
But does it? Does the finding of such a dissociation really demand explanation in terms of multiple memory systems? After all, both recognition and categorization are aspects of declarative memory, as defined by Winograd (1975) and Anderson (in the ACT model) as factual knowledge, with truth value (i.e., it is either true or false) that can be given a propositional (or, perhaps, imagistic) representation. From this point of view, recognition requires access to declarative knowledge about one's own experiences, or what Tulving calls episodic memory, while categorization requires access to declarative knowledge about the world in general, or what Tulving calls semantic memory. While Tulving and Schacter have suggested that episodic and semantic memory are processed by different memory systems, just as explicit and implicit memory are, other theorists view episodic and semantic memory as different aspects of a single declarative memory system. For example, Hintzman showed that MINERVA2, which encodes traces of individual experiences without abstracting any generalized conceptual representations (and thus has only episodic, not semantic, memory), can successfully simulate actual dot-pattern classification performance.
Along the same lines, Nosofsky and Zaki
(1998) suggested that the dissociation between recognition and
classification observed by Knowlton and Squire could be
produced in a computer simulation of memory that assumed the
existence of just a single memory system. They created the
Generalized Context Model (GCM), a variant on Hintzman's
MINERVA2, in which representations of past experience are
stored in a single memory system. GCM performs both
recognition and classification in exactly the same way.
GCM is, in turn, based on an earlier exemplar model of
categorization that assumes only a single memory system
(Nosofsky, 1988, 1991).
So, in both cases, performance involves matching a probe to a stored instance -- whether it's an episode or a category exemplar. Knowledge about concrete experiences and knowledge about abstract categories are both stored in the same memory system. The only difference is that the criterion for event-recognition is different from the criterion for categorization. In fact, Nosofsky & Zaki assumed that the system had a higher threshold for event recognition than for item categorization. Assuming that the effect of amnesia is to lower the sensitivity of the comparison process, this will impair recognition but leave enough information available in memory to support categorization.
In
their
experiment, Nosofsky and Zaki simulated amnesia, defined as
degraded explicit memory, in normal, neurologically intact
subjects by increasing the retention interval for the
recognition test. This manipulation effectively raised
the threshold for both episodic recognition and categorization
-- effectively, making it "harder" for the system to reach the
criterion required for a positive judgment. Remarkably, as
shown in the figure, this simple expedient led GCM to
precisely duplicate the performance of the amnesics and
controls studied by Knowlton & Squire. Nosofsky and Zaki
obtained similar results with a probabilistic classification
task studied by Knowlton and her colleagues, and which had
also yielded a dissociation between recognition and
classification.
Nosofsky and Zaki
(1998) went on to apply their model to the categorization data
collected by Knowlton and Squire (1993). Applying their
single-system exemplar model to the dot task, they found that
the greater the distance of a probe from the category
prototype, the lower is its similarity to old, studied items
(according to the model). That is, the model performed
just like normal human subjects would be expected to do.
And,
for that matter,
the GCM model performed just like Knowlton and Squire's
amnesic patients. In fact, the match between the
simulation and the actual performance of K&S's subjects
was downright uncanny.
The implication of the exemplar model is that both normal and amnesic performance on both recognition and categorization tasks can be mediated by a single memory system that has different criteria for recognition judgments, and different levels of sensitivity for amnesic and normal subjects. This single-store exemplar model gives a good fit when compared against the performance of amnesic patients. Therefore, the dissociation observed between event recognition and item categorization does not require separate memory systems mediating performance on the two tasks.
Most recently, Zaki and Nosofsky (2001) successfully simulated another amnesic dissociation, between recognition and classification of cartoon-like artificial animals called "Peggles" composed of a particular combination of nine binary dimensions, such as left- versus down-facing head, dog-like versus pig-like face, and striped versus spotted markings. In the original experiment, amnesic patients classified Peggles at roughly normal levels (63.9% correct versus 73.8% for controls, despite a profound inability to recall the animals' features (49.2% correct versus 81.1% for the controls). Because the animals and their features were highly verbalizable in a way that the dot patterns were not, Reed, Squire, and their colleagues (1999) argued that this experiment provided even more compelling evidence that recognition and categorization were mediated by separate brain systems. Nevertheless, Zaki and Nosofsky (2003) found that the MINERVA2-like GCM model was able to successfully simulate that performance as well.
Taken together, these results constitute a kind of "existence proof" that a single memory system can duplicate the kinds of dissociations that are frequently attributed to the operation of multiple memory systems. Just as episodic and semantic memories can be represented in a single memory system, so explicit and implicit expressions of episodic memory can be mediated by a single memory system. In an exemplar model such as MINERVA2 or GCM, recognition occurs only if a probe matches some specific item already stored in memory, and recognition fails if such a match fails to occur within some specified period of time. But categorization occurs if a probe matches any stored exemplar of a known category. Obviously, then, categorization is in some sense "easier" than recognition. So long as this is the case, categorization will succeed when recognition fails -- creating dissociations such as those observed by Knowlton and Squire in their various experiments. Just as Roediger's transfer-appropriate processing view argues that dissociations between explicit and implicit memory are created by different processes operating on knowledge represented in a single memory system, so Nosofsky and Zaki argue that they are created by differences in "difficulty" in the explicit and implicit tasks.
One problem with the Nosofsky and Zaki studies is that while they were able to simulate amnesia by raising the threshold for a positive response, GCM was never completely amnesic and still retained some ability, however weak, to distinguish between old and new items. However, there are some amnesic patients who appear to have absolutely no explicit memory at all, but still appear to perform normally on tests of implicit memory.
For example,
Squire and Knowlton found that patient E.P., who is amnesic as
a result of herpes simplex encephalitis, performs
normally on tests of dot-pattern categorization even though
his recognition memory is strictly at chance levels. E.P. also
performed normally on the classification of Peggles. Such
findings are apparently inconsistent with single-system models
such as MINERVA2 and GCM, which require at least some minimal
sparing of recognition -- e.g., a recognition threshold lower
than infinity -- in order to perform. If, in GCM, we degrade
recognition completely, so that no exemplar information is
stored at all, categorization must also fall to chance levels.
Because E.P. can categorize things he cannot recognize, it
might be that there are two memory systems after all.
So, the Squire and Knowlton argument is that the case of E.P. is actually inconsistent with the exemplar model, which requires only a relative impairment of recognition, leaving some recognition ability intact. According to the GCM model, if you degrade recognition completely, as is the case in E.P., categorization also must fall to chance. Therefore, since E.P. does show normal levels of categorization, despite chance levels of recognition memory, there must be two memory systems after all -- one for event recognition, and one for category learning.
However -- and there is always a "however", isn't there? -- this counterargument has problems of its own.
In the first place, there is a real problem with the categorization tests used by Knowlton and Squire in their various studies: subjects can perform at above-chance levels on the classification test even if they have never been exposed to any examples during the study phase. In order to understand how this might be so, consider first the test stimuli used in the original study by Knowlton and Squire, examples of which are displayed in the figure. Recall that, for the recognition test, subjects studied and were tested on five patterns that were each a high distortion of a different prototype -- in other words, none of them looked very much like any of the others. But in the categorization test, half the items were examples of the category, while the other half were not -- in other words, half of the items looked like each other.
So, just to begin with, there's a confound between the structure of the recognition test and that of the categorization test.
But the more important point is that subjects in the categorization test could perform relatively well simply by identifying as a category member any test stimulus that looked like another test stimulus they had recently seen. Importantly, this strategy does not require long-term memory of the sort that is impaired in E.P. and other amnesic patients. It relies only on short-term or working memory, and this form of memory is unimpaired in E.P., just as it is unimpaired in other amnesic patients.
In fact, Knowlton and Squire themselves had reported a second experiment in which normal subjects who received no training classified dot patterns at levels that were only numerically above chance, 53.7%, compared to 64.4% for amnesic patients and intact controls who had actually been exposed to the stimuli. Similarly, Reed et al. reported that untrained subjects classified Peggles at only chance levels. Taken together, these findings argue against the hypothesis that E.P.'s classification performance could have been mediated by a strategy based on primary memory. However, the specific instructions given to subjects are very important here. Both Knowlton and Squire and Reed et al. instructed their subjects to "imagine" that they had been exposed to the dot patterns. Because they had clearly not been exposed to anything at all, the demand characteristics implicit in these instructions might well have communicated to the subjects that they were in a control group of some sort, and induced them to behave randomly.
Quite
a different
approach was taken by Palmeri and Flannery (1999). These
investigators created a clever laboratory deception in which
in which the subjects were told that they had been
subliminally exposed to dot patterns belonging to a particular
category in the course of an experiment involving the
identification of visually presented words. These researchers
were thus able to capitalize on the prevailing cultural myths
surrounding subliminal influence to induce subjects to behave
as if they really had been exposed to the
stimuli. Under these circumstances, "recognition" was at
chance levels, as it was for E.P. However, categorization was
significantly above chance at 60.4%, a level of performance
that is comparable to that reported by Knowlton and Squire for
amnesic patients, and for E.P.
Using this same mock subliminal-perception procedure, plus a bonus of $5 for above-chance performance, Zaki and Nosofsky (2003) reported that many of their subjects, 38% to 62% depending on how they counted, were able to classify Peggles correctly despite never having been exposed to any training instances. Far from requiring a separate memory system, then, it is clear that the categorization performance of amnesic patients could be mediated by a single memory system after all, so long as the category task makes few demands on memory resources. Palmeri and Flannery (2002) also showed that a single-system exemplar model of classification could account for subjects' learning of a complex quadratic role, and also for artificial grammar learning.
Similarly, Kinder & Shanks (2001) were able to simulate performance on an artificial grammar learning task with a connectionist model that also assumes only a single memory system.
The implications of the Palmeri and Flannery experiment are clear enough. Successful performance on the categorization task used by Knowlton & Squire (1993) does not require previous category learning. Instead, subjects can induce the category based on their experience of the test probes. Accordingly, the "dissociation" between recognition and categorization claimed by Knowlton and Squire (1993) is actually uninformative about the memory systems (whether in the mind or the brain) underlying task performance.
For
a while, the final word on this matter came from a review of "Category Learning
and Memory Systems" by Ashby and O'Brien (2004). They
point out that categorization obviously depends on memory,
both to support the learning process and to store
representations of categories themselves. They also
point out that there are different kinds of categories (or, at
least, different kinds of categorization tasks), as
well as different kinds of memory. Therefore, they
hypothesize that performance on different kinds of
categorization tasks is mediated by different kinds of
memory. They hoped that neuroscientific data might be
informative about whether category learning is, in fact,
mediated by multiple, qualitatively different memory
systems. But after reviewing the kind of evidence
summarized above, they concluded that such a resolution was
not yet possible.
But the argument didn't
stop there (it never does).
Bozoki
et al. (2006) performed a conceptual replication of the
Knowlton & Squire (1993) study, with different
stimulus materials (artificial animals known as "Peggles"
rather than dot-patterns). Palmeri
and Flannery (1999) and shown that
subjects could learn category structure simply during
the test trials themselves, relying solely on working
memory. Bozoki et al. agreed
that this could occur,
but argued that long-term memory conferred an extra
advantage, over and above working memory.
After subtracting out the contributions of working
memory, they found that patients with mild
Alzheimer's Disease also had learned something
about the categories during the training trials. This, they argued, was a
reflection of implicit category learning, and
thus constituted evidence for multiple systems
for learning and memory. One system,
supporting explicit recognition memory, was
impaired; the other system, supporting
category learning, was spared.
Following the Bozoki et al. (2006) study, Smith (2008) reviewed the entire literature and reasserted (as stated in the title of his paper) "The Case for Implicit Category Learning". In this paper, Smith reviewed five different criticisms of the category-learning research, and found none of them completely convincing.
But you know, deep in your heart of hearts, that despite the neuroscientific appeal of the doctrine of modularity, the single-system view has an awful lot going for it. Whatever the truth turns out to be, neuroscientific data is unlikely to be decisive in this respect, because, by its very nature, biological data can't constrain psychological theory. Instead, the proper interpretation of biological function depends on the prior existence of a valid psychological theory.
Returning to the notion of converging strategies, it appears that, whether you're a computational modeler or a cognitive neuroscientist, behavioral experiments show you what to look for. The investigator must have a proper understanding of the subject's task at the psychological level of analysis before s/he can hope to identify the neural substrates of the mental process at issue. Otherwise, we do not really gain any insight into what the brain is doing. Neuroscience has no privileged status as a road to psychological theory, but computational models may constrain both behavioral and neuroscientific analyses of mental structure and process. This is because computational models constitute formal theories of the underlying processes, forcing us to dot all the is and cross all the t, and allowing us no room for hand-waving. Computational models permit us to compare simulations against actual empirical data, and also to compare competing simulations against each other, and thereby test plausible alternative theories.
In the end, there is a symbiotic relationship among behavioral methods, neuroscientific analyses, and computational modeling. Each method makes its own unique contribution to the study of memory, cognition, and the mind. But in the end, behavioral data trumps everything, because it provides grist for the computational mill, and generates the psychological background for interpreting neuroscientific results.
This page last modified
12/18/2023.