Fractals: The Mandelbrot Set
Construction:

The Mandelbrot set is the set of all complex numbers c
such that iterating z <= z^2 + c does not ascend to infinity,
starting with z=0.
The terms z and c are complex numbers (see Note 1 for an overview of complex numbers, if necessary). "Ascend to infinity" means that z will continue to grow with each iteration; in calculus terms, it means that z diverges; more on this, as well as the initial condition z=0, later. I will proceed with explaining simply how to graph the set, and place explanations for the mathematical intricacies in footnotes for those curious.
We could probably find a few elements in the Mandelbrot set by pencil and paper, but in order to crank out enough iterations to produce even a semi-decent graph before dying of either old age or a mental segmentation fault, we will want to determine the elements of the Mandelbrot set using a simple computer program. I will use Java-like pseudocode. Let us first declare a complex number class complexNumber:
// A class for complex numbers.
class complexNumber {
private double a, b; // a and b from the form a + bi
public complexNumber(double realNumber, double imaginaryNumber) { // Class constructor.
a = realNumber; b = imaginaryNumber;
}
public double realPart() { // Returns real value a.
return a;
}
public double imaginaryPart() { // Returns imaginary value b.
return b;
}
public double absoluteValue() { // Returns vector magnitude, sqrt(a^2 + b^2).
return (sqrt(exp(a,2)) + exp(b,2)));
}
}
Each object in the complexNumber class has two double-precision fields, a and b. The functions are self-explanatory.
With the one sentence description of the Mandelbrot set at the top of the page, we will write a function checkMandelbrotElement() for checking whether c is a member of the Mandelbrot set. Let z be a local free variable, and c be an input constant. We initialize z to 0(see Note 2 for an explanation of this initialization). Following the described algorithm, we would start by reassigning z to the value of z^2 + c = 0^2 + c = c. Then we reassign z to the sum of c and the square of the new z we had just computed (e.g. the second iteration is z = c^2 + c, third iteration is z = (c^2 + c)^2 + c, fourth is z = [(c^2 + c)^2 + c]^2 + c, etc.) ... and continue doing this for some large number of iterations N. This can be done with a for loop. As for an exit condition for our loop, with each iteration we will check the value of |z| and see if it is greater than 2. If it is, the value of z will diverge to infinity in further iterations (see Note 3 for a proof), and we thus we know that c is not a solution. Otherwise, we iterate further; if |z| remains less than or equal to 2 for all N iterations, c is a solution. Pseudocode:
checkMandelbrotElement(int N, complexNumber c) {
for (int i=N, complexNumber z=0; i>=0; i--) {
if (i == 0) {
inTheSet(c);
} else if (z.absoluteValue() > 2) {
notInTheSet(z);
break;
} else {
z = z^2 + c;
}
}
}
The program implements the described algorithm, taking as input the number of iterations N and the complex number c. Reexplaining the algorithm in terms of the code above, we declare a local complexNumber-typed variable z on which we do the iterative reassignments necessary for checking if c is a solution. These iterations are done in a simple for loop which is set to execute a maximum of N iterations. If the magnitude of z at any iteration is greater than 2, we can immediately mark z as not being in the solution set, and exit the loop with break(). Otherwise, we reassign z and continue looping; if |z| is never greater than 2 after N iterations, the computer finally evaluates the first if statement (whose condition is true when i is 0), marking z as a solution with function "inTheSet(z)," and then exits the loop normally as i is decremented to -1.
So we have a function that checks whether any one complex number c is in the set. Now we will want to apply this function to many values of c to get a better picture of what values are in the set. We can have a computer execute checkMandelbrotElement() on a large domain in the complex plane - for instance, the set of all pixels on a a computer screen, where pixels represent complex numbers (horizontal indices mapping to their real parts on the complex plane, and vertical indices mapping to their imaginary parts on a complex plane:
// True monitors do not have the same width as height, but we will assume so to make computation easier.
#define monitorWidth 800;
#define monitorHeight 800;
generateMandelbrot(complexNumber c, int N) {
int pixels[i][j];
for (i=0; i<=monitorWidth; i++) {
for (j=0; j<=height, j++) {
// Note 4 explains subtracting (i,j) by 400 and dividing by 200
complexNumber z = new complexNumber( ((i-400)/200), ((j-400)/200) );
checkMandelbrotElement(N, z, c);
}
}

Thus we now have a program which checks if each pixel on a screen is a member of the Mandelbrot set dictated by the parameters c and N given to function generateMandelbrot(), c being the parameter space and N giving greater levels of detail for greater values. We could graph this set on a computer screen by assigning a certain color to each pixel based on whether they are in the set or not. In the first code segment, function checkMandelbrotElement() also calls functions inTheSet() and notInTheSet(), which mark whether or not the complex plane vector corresponding to a particular pixel is in the Mandelbrot set. Let us say that inTheSet() colors pixels black, while notInTheSet() colors them white. Following this scheme, the code we have written would generate a picture similar to that shown on the left, displaying the distinctive shape of the Mandelbrot set.
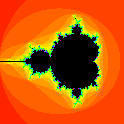
How can we get more colors? The code above only puts pixels in one of two categories, in the set, or not in the set. To get more categories, we could make a more complicated program that assigns a color to pixel c according to the value of z for that c after N iterations. Some values will quickly converge to zero, some will reach an cyclic equilibrium, some will immediately diverge to infinity. These growth differences allow for such divisions as "infinitely small", "relatively small", "relatively large", and "infinitely large", each mapping to a different color; we could even generate a 3-dimensional graph by mapping pixel values to heights. This concludes the construction.
Mandelbrot Set Variations:
The recursive function z <= z2 + c can be considered a special case of the formula z <= zn + c, where n is preferably a positive integer. Below are graphs of this more general formula for n = 2, 3, and 4. Fractals can also be made from the formula z <= z-barn + c, where z-bar is the complex conjugate of z; such fractals are called Mandelbar sets. Below are graphs of these formulae for n = 2, 3, and 4. Notice the pattern of expansion in z <= zn + c. The growth pattern in the Mandelbar set is more obvious, each shape resembling a polygon with n+1 sides, and flaring at the corners.
| n |
z <= zn + c |
z <= z-barn + c |
| 2 |
 |
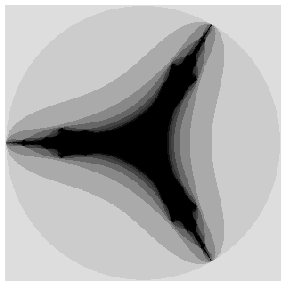 |
| 3 |
 |
 |
| 4 |
 |
 |
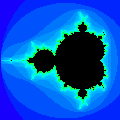
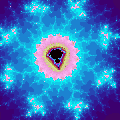
We end our discussion of the Mandelbrot set with two pictures. The left picture (leftmost) views the entire Mandelbrot set. The right picture is actually the highly magnified image of a small fraction of the first picture. Look closely at the center of the second picture, and you can see a small black figure identical to the leftmost picture but reduced in size. Click on the file link below to witness this cyclic repetition of the set's complexities. The fantastic 12-second MPEG clip starts at topmost view of the Mandelbrot set, and zooms in, showing reductions of the same figure we started with along the way. Highly recommended.
Update: Looks like I have lost the aformentioned file. More precisely, inst.eecs.berkeley.edu erased it. But here is a much better one, produced by Thomas Marsh and Jan Hubicka of Xaos. Includes many zoom-ins. The clip cannot be fast forwarded, so just watch the whole thing patiently.
MPEG Tutorial On The Mandelbrot Set
MPEG Tutorial On The Julia Set
Footnotes:
- Note 1: Complex Numbers
Complex numbers are numbers expressed in the form a + bi, where a and b are real numbers, and i is the imaginary number, the square root of -1. In fractal geometry, we graph points against two axes, a horizontal real axis and a vertical imaginary axis; this plane is often called the complex plane (as opposed to the xy plane, where x and y are both real). Hence, 4 + 5i can be graphed on an complex plane as corresponding to point (4,5). The absolute value of a complex number is simply sqrt(a^2 + b^2), which corresponds to the hypotenuese of the triangle formed by the real and imaginary parts on the complex plane.
Return to Note 1 context
- Note 1: z=0 Initialization
We start with z equal to zero because it is the critical point of z^2 + c (from introductory calculus: a point where d/dz (z^2 + c) = 0). If the recursive function was z = (z-1)^2 + c, we would start with z = 1 (0 = d/dz [(z-1)^2 + c] = [d/dz (z-1)^2] + 0 = 2(z-1) -> 2z = 2 -> z = 1). In some cases there may be multiple critical values, so they should all be tested.
Mathematician Pierre Fatou (1878-1929) showed that every attracting cycle for a polynomial or rational function attracts at least one critical point. Thus, testing the critical point shows if there is any stable attractive cycle. Return to Note 2 context
- Note 3: Diverging Condition
In the coding of the checkMandelbrotElement() function, we say that if |z| is ever greater than 2, we can be assured that the z sequence corresponding to parameter c will diverge, and c is thus not in the set. Proof: If |z| > 2, then |z^2 + c| >= |z^2| - |c| > 2|z| - |c|. If |z| >= |c|, then 2|z| - |c| > |z|. So, if |z| > 2 and |z| >= c, then |z^2 + c| > |z|, and thus the sequence is increasing. (It takes a little more work to prove that the sequence is unbounded and diverges.)
From this line of reasoning, it follows that the bounds of the Mandelbrot set are within |c| <= 2. In the first iteration, z = 0^2 + c = c, so if |c| > 2, the sequence diverges. Return to Note 3 context
- Note 4: Computer screen scaling
The explanation for subtracting 200 from ( i , j ) and then dividing by 400 stems from the proof given in Note 3. Since the bounds of the Mandelbrot set are |c| <= 2, we want the dimensions of our graph to be [-2,2] (real axis) by [-2,2] (imaginary axis) - a larger graphing space would be a waste of space. However, the pixels on a computer monitor are indexed on a [0,monitorWidth] by [0,monitorHeight] cross product set, with (0,0) being the upper-left corner. Hence we have to do some arithmetic operations on a pixel's indices prior to making a useful complex number corresponding to that pixel. To shift the origin to the center of the screen, we subtract half of monitorWidth from i and then divide this difference by a fourth of monitorWidth, and subtract half of monitorHeight from j and then divide this difference by a fourth monitorHeight:
complexNumber z = new complexNumber( (i-(monitorWidth/2))/(monitorWidth/4) , (j-(monitorHeight/2))/(monitorHeight/4) );
So, if monitorWidth = monitorHeight = 800, then i=0 -> (0-400)/(200) = -2; i=800 -> (800-400)/(200) = 2; j=0 -> (0-400)/(200) = -2; j=0 -> (800-400)/(200) = 2. Thus we produce only complex numbers in the cross product of [-2, 2] and [2, 2]. Return to Note 4 context
William Wu, Copyright 2000-2002 ©. All rights reserved.
















