At a certain level many-body localization (MBL) can be viewed as the extension of Anderson localization to the case of a many-body system of interacting particles. Many-body localized systems decoupled from an external environment are not able to serve as their own heat bath and therefore fail to reach thermal equilibrium; they are the only generic exception we know to conventional ergodic time evolution. Because of the failure to thermalize, quantum correlations persist in MBL systems and play a crucial role in the dynamics even at long time scales. This is related to the fact that not only matter and energy are localized in this state, but also quantum information remains partially localized. Much of my recent work has been devoted to understanding the nature of the dynamics in the MBL state and to characterizing the phase transition between this state and an ergodic fluid.
This is a recent review I have written on the dynamics in the MBL phase
Ehud Altman and Ronen Vosk, Annual Rev. of Cond. Mat. Phys. Vol. 6: 383-409 (2015)
These are my Les Houches lecture notes on non equilibrium phenomena in ultra-cold atomic systems: arXiv:1512.00870.
Here are selected problems I have worked on in relation to MBL, non-equilibrium dynamics and thermalization.
Theory of the Many-Body Localization Transition
(with Ronen Vosk and David Huse)
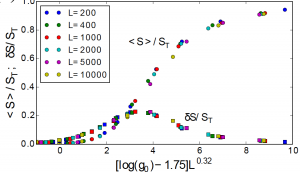
We developed a new renormalization group framework to describe critical properties near the transition from a many-body localized state to a thermal fluid. Interestingly, entanglement emerges as the natural scaling variable in this approach; the RG predicts a universal change of the entanglement entropy from an area law to a thermal volume law via an intriguing critical point with non-trivial scaling exponents and where the distribution of entanglement becomes maximally broad. The RG, applied to one dimensional systems, also predicts sub diffusive transport with a diverging dynamical exponent z at the critical point.
Figure: Scaling collapse of eigenstate entanglement entropy and it’s fluctuations across the MBL critical point.
Ronen Vosk, David A. Huse, and Ehud Altman Phys. Rev. X 5, 031032 (2015)
Renormalization group approach to the MBL state
(with Vosk and other collaborators listed below)
 We developed a dynamical strong disorder RG to describe the dynamics and spectral properties in the MBL phase. The MBL state is seen to be a stable fixed point of the RG characterized by an infinite set of quasi-local integrals of motion (LIOM), which are gradually revealed in the course of the RG flow. The constrained dynamics subject to the local conservation laws is the underlying reason for failure of ergodicity.
We developed a dynamical strong disorder RG to describe the dynamics and spectral properties in the MBL phase. The MBL state is seen to be a stable fixed point of the RG characterized by an infinite set of quasi-local integrals of motion (LIOM), which are gradually revealed in the course of the RG flow. The constrained dynamics subject to the local conservation laws is the underlying reason for failure of ergodicity.
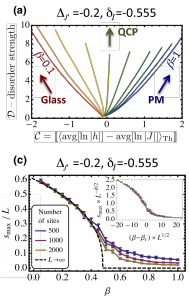
It is now understood that MBL can protect quantum orders such as broken symmetries and topologcial order even in high energy many-body eigenstates. The dynamical RG and closely related RSRG-X approaches allow to study the universal dynamics characterizing critical points that separate distinct MBL states.
Figure: RSRG-X results for a dynamical critical point between an MBL paramagnet and MBL Ising glass. Top: the RG flow of the disorder distributions; bottom: finite size scaling collapse of the order parameter.
R. Vosk and E. Altman PRL 110, 067204 (2013)
R. Vosk and E. Altman PRL 112, 217204 (2014)
D. Pekker, G., E. Altman, E. Demler, and V. Oganesyan PRX 4, 011052 (2014)
Coherent edge states at high energies protected by topology and localization
(with Bahri, Vosk and Vishwanath)
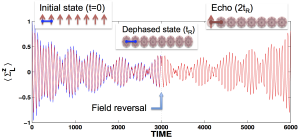 We extended the concept of a topological state of matter, usually sharply defined only in the quantum ground state, to highly excited states of a correlated quantum system, which is in a many-body localized phase. Specifically we considered a 1 dimensional system which realizes a symmetry protected topological phase. We demonstrate that in this case the bulk topology can give rise to a protected q-bit at the edge, surprisingly, even when the system is very ‘hot’ and strongly coupled to the degrees of freedom making up the q-bit. Our work goes beyond parallel works establishing the existence of such phases by demonstrating a quantum coherent response, without the need to cool into the ground state of the system (figure). This result is enabled by a combination of topology and strong disorder, which preserve the topological structure, not only in the ground states, but in all of the exponentially many states of the spectrum.
We extended the concept of a topological state of matter, usually sharply defined only in the quantum ground state, to highly excited states of a correlated quantum system, which is in a many-body localized phase. Specifically we considered a 1 dimensional system which realizes a symmetry protected topological phase. We demonstrate that in this case the bulk topology can give rise to a protected q-bit at the edge, surprisingly, even when the system is very ‘hot’ and strongly coupled to the degrees of freedom making up the q-bit. Our work goes beyond parallel works establishing the existence of such phases by demonstrating a quantum coherent response, without the need to cool into the ground state of the system (figure). This result is enabled by a combination of topology and strong disorder, which preserve the topological structure, not only in the ground states, but in all of the exponentially many states of the spectrum.
Y. Bahri, R. Vosk, E. Altman and A. Vishwanath, arXiv:1307.4092
Experimental Evidence of Many Body Localization
(with Vosk, Fischer and I. Bloch’s experimental group at LMU)
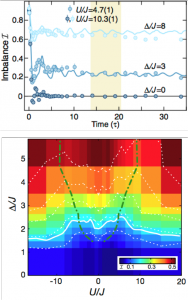 We have provided theoretical guidance and interpretation to an experiment showing the first clear evidence of many body localization and the associated breaking of ergodicity. The experiment, done by Immanuel Bloch’s group at LMU (Munich), identified the MBL transition through the relaxation dynamics of an initially prepared charge density wave. For sufficiently weak disorder, the time evolution appears ergodic and thermalizing, erasing all initial ordering, whereas above a critical disorder strength, a substantial portion of the initial ordering persists. The non-ergodic saturation of the charge density wave is demonstrated in the first figure to the right showing both numerical and experimental results. The second figure shows the experimentally determined phase diagram in the space of disorder Δ and interaction strength U (MBL above the white line).
We have provided theoretical guidance and interpretation to an experiment showing the first clear evidence of many body localization and the associated breaking of ergodicity. The experiment, done by Immanuel Bloch’s group at LMU (Munich), identified the MBL transition through the relaxation dynamics of an initially prepared charge density wave. For sufficiently weak disorder, the time evolution appears ergodic and thermalizing, erasing all initial ordering, whereas above a critical disorder strength, a substantial portion of the initial ordering persists. The non-ergodic saturation of the charge density wave is demonstrated in the first figure to the right showing both numerical and experimental results. The second figure shows the experimentally determined phase diagram in the space of disorder Δ and interaction strength U (MBL above the white line).
M. Schreiber et. al. Science 349, 842-845 (2015)
Many-Body delocalization of particles by coupling to marginally localized phonons
(with S. Banerjee)
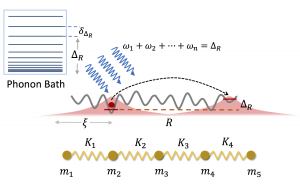
We investigate the effect of coupling Anderson localized particles in one dimension to a system of marginally localized phonons having a symmetry protected delocalized mode at zero frequency. This situation is naturally realized for electrons coupled to phonons in a disordered nano-wire as well as for ultra-cold fermions coupled to phonons of a superfluid in a one dimensional disordered trap. To determine if the coupled system can be many-body localized we analyze the phonon-mediated hopping transport for both the weak and strong coupling regimes. We show that the usual variable- range hopping mechanism involving a low-order phonon processes is ineffective at low temperature due to discreteness of the bath at the required energy. Instead, the system thermalizes through a many-body process involving exchange of a diverging number n ∝ −logT of phonons in the low temperature limit. This effect leads to a highly singular prefactor to Mott’s well known formula and strongly suppresses the variable range hopping rate.
S. Banerjee and E. Altman, Phys. Rev. Lett. 116, 116601 (2016)
Dynamics of a many-body localized system weakly coupled to a bath
(with M. Fischer and M. Maksymenko)
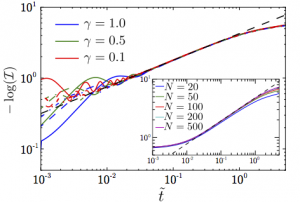 Coupling a many-body-localized system to a dissipative bath necessarily leads to delocalization. Here, we investigate the nature of the ensuing relaxation dynamics and the information it holds on the many-body-localized state. We formulate the quantum master equation (Lindblad) in terms of the local integrals of motion of the underlying MBL Hamiltonian. This allows to map the quantum evolution deep in the localized state to tractable classical rate equations. Using the effective model we can analytically obtain slow (stretched exponential) relaxation dynamics of the MBL integrals of motion.
Coupling a many-body-localized system to a dissipative bath necessarily leads to delocalization. Here, we investigate the nature of the ensuing relaxation dynamics and the information it holds on the many-body-localized state. We formulate the quantum master equation (Lindblad) in terms of the local integrals of motion of the underlying MBL Hamiltonian. This allows to map the quantum evolution deep in the localized state to tractable classical rate equations. Using the effective model we can analytically obtain slow (stretched exponential) relaxation dynamics of the MBL integrals of motion.