In recent years there has been substantial progress in experiments with many-body quantum systems strongly coupled to light. A case in point are fluids of exciton-polariton excitations of semiconductor quantum-wells in an optical cavity. Pumping with light to overcome photon loss, drives these many-body systems into a non-equilibrium steady states which we seek to understand. These are some of the questions we attempt to address: can the classification of equilibrium phases of matter be generalized to driven steady states; Do phase transitions exist in such systems, and if so how do we characterize them? Can a scaling approach be applied ? Can quantum interference effects survive and dominate certain states of driven systems? Below are brief descriptions of selected projects.
Fate of condensation and superfluidity in 2d driven open systems
(With S. Diehl, L. Sieberer, J. Toner, G. Wachtel and others)
Motivated by experiments that show signatures of condensation of exciton-polaritons in two dimensional semiconductor quantum wells we investigated how the non-equilibrium conditions inherent in this system affect the condensate and superfluid properties.
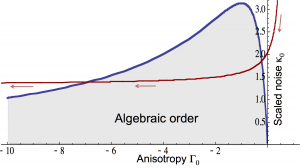 Condensation — We have shown that driven condensates have a universal long-wavelength description, fundamentally different from that of equilibrium quantum-fluids. It is given by the well known Kardar-Parisi-Zhang (KPZ) equation, originally developed as a description of randomly growing interfaces. The non linear term in this theory, allowed only due to the drive, is always relevant in two dimensions and leads to disordering of the condensate beyond an emergent long distance scale unless the underlying microscopic dispersion is strongly anisotropic. In the latter case we find a surprising reentrant effect: with increasing pump power the system transitions into a condensed state at a critical pump power but then goes back to the normal state beyond a second critical power. The red line in the figure (from Ref. [1]) shows a possible experimental trajectory.
Condensation — We have shown that driven condensates have a universal long-wavelength description, fundamentally different from that of equilibrium quantum-fluids. It is given by the well known Kardar-Parisi-Zhang (KPZ) equation, originally developed as a description of randomly growing interfaces. The non linear term in this theory, allowed only due to the drive, is always relevant in two dimensions and leads to disordering of the condensate beyond an emergent long distance scale unless the underlying microscopic dispersion is strongly anisotropic. In the latter case we find a surprising reentrant effect: with increasing pump power the system transitions into a condensed state at a critical pump power but then goes back to the normal state beyond a second critical power. The red line in the figure (from Ref. [1]) shows a possible experimental trajectory.
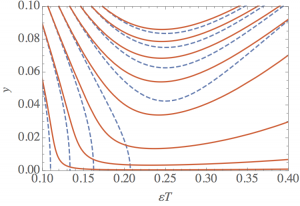 Superfluidity — The KPZ equation for the phase dynamics of the condensate is different from the standard KPZ in that the phase field is compact and thus supports topological defects (vortices). To characterize the superfluid properties of the polariton fluid we account for the vortices by developing a dual description of the compact KPZ equation in terms of non-linear electrodynamics with charges. Using the dual theory we derive renormalization group equations that describe vortex unbinding in the media. When the non-equilibirum drive is turned off, the KPZ non-linearity vanishes and the RG flow gives the usual Kosterlitz-Thouless (KT) transition (dashed lines in the figure). On the other hand, with the KPZ non-linearity vortices always unbind as shown by the red trajectories (taken from Ref. [2]). We predict the finite size scaling behavior of the superfluid stiffness in the crossover governed by vortex unbinding, which is very different from the scaling associated with the conventional KT transition.
Superfluidity — The KPZ equation for the phase dynamics of the condensate is different from the standard KPZ in that the phase field is compact and thus supports topological defects (vortices). To characterize the superfluid properties of the polariton fluid we account for the vortices by developing a dual description of the compact KPZ equation in terms of non-linear electrodynamics with charges. Using the dual theory we derive renormalization group equations that describe vortex unbinding in the media. When the non-equilibirum drive is turned off, the KPZ non-linearity vanishes and the RG flow gives the usual Kosterlitz-Thouless (KT) transition (dashed lines in the figure). On the other hand, with the KPZ non-linearity vortices always unbind as shown by the red trajectories (taken from Ref. [2]). We predict the finite size scaling behavior of the superfluid stiffness in the crossover governed by vortex unbinding, which is very different from the scaling associated with the conventional KT transition.
[1] E. Altman, L. Sieberer, L. Chen, S. Diehl and J. Toner, ”Two-dimensional superfluidity of exciton-polaritons requires strong anisotropy”, Phys. Rev. X 5, 011017 (2015).
[2] G. Wachtel, L. Sieberer, S. Diehl and E. Altman, “Electrodynamic duality and vortex unbinding in driven-dissipative condensates”, Phys. Rev. B 94, 104520 (2016)
[3] L. Sieberer, G. Wachtel, E. Altman and S. Diehl, “Lattice duality for the compact Kardar-Parisi-Zhang equation”, Phys. Rev. B 94, 104521 (2016)
[4] J. Keeling, L. M. Sieberer, E. Altman, L. Chen, S. Diehl, J. Toner, “Superfluidity and Phase Correlations of Driven Dissipative Condensates”, arXiv:1601.04495. To be published as a book chapter.
Non equilibrium condensation transition in driven-dissipative Bose fluids
(With S. Diehl, L. Sieberer and S. Huber)
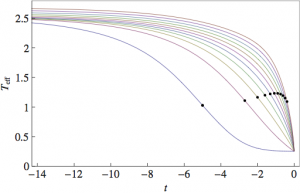 Here we looked at a driven condensate in 3d, which unlike the 2d case, does sustain a broken symmetry state. We specifically addressed the superlfuid transition in this case within a Keldysh field theory. This allowed to express thermal equilibrium as a symmetry of the Keldysh action. At the microscopic level the system is out of equilibrium and this symmetry is broken. However, we showed that effective equilibrium is established as an emergent symmetry at low frequencies. Hence all static properties appear identical to the corresponding thermal phase transition. On the other hand, dynamic correlations bear witness to the non-equilibrium physics. For example, the effective temperature appearing in fluctuation-dissipation relations has the frequency dependence: T(ω)=T0(1+Aωη). The critical exponent η describes the the rate at which effective equilibrium is established.
Here we looked at a driven condensate in 3d, which unlike the 2d case, does sustain a broken symmetry state. We specifically addressed the superlfuid transition in this case within a Keldysh field theory. This allowed to express thermal equilibrium as a symmetry of the Keldysh action. At the microscopic level the system is out of equilibrium and this symmetry is broken. However, we showed that effective equilibrium is established as an emergent symmetry at low frequencies. Hence all static properties appear identical to the corresponding thermal phase transition. On the other hand, dynamic correlations bear witness to the non-equilibrium physics. For example, the effective temperature appearing in fluctuation-dissipation relations has the frequency dependence: T(ω)=T0(1+Aωη). The critical exponent η describes the the rate at which effective equilibrium is established.
Figure: RG flow of the effective temperature with the frequency scale Ω measured by t=log(Ω/Ω0) for various microscopic conditions.
[1] L. M. Sieberer, S. D. Huber, E. Altman, S. Diehl, “Dynamical Critical Phenomena in Driven-Dissipative Systems”, Phys. Rev. Lett. 110, 195301 (2013).
[2] L. M. Sieberer, S. D. Huber, E. Altman, S. Diehl, “Non-equilibrium Functional Renormalization for Driven-Dissipative Bose-Einstein Condensation”, Phys. Rev. B 89, 134310 (2014).
Quantum criticality in dissipative systems driven by non-equilibrium noise
(With E. Dala-Torre, E. Demler and T. Giamarchi)
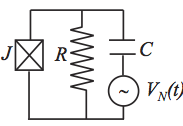
We have investigated the effect of non-equilibrium noise sources on quantum critical points using a Keldysh field theory approach. Our framework and results pertain to a number important physical situations in electronic as well as cold atom systems. For example we considered how 1/f noise affects the superconductor to metal quantum phase transition in a resistively shunted Josephson junction (right). We found that the noise shifts the transition away from the universal value of the shunt resistance (h/4e²) and opens the critical point into a crossover governed by a new non-equilibrium fixed-point. An effective thermal equilibrium is established in the low frequency limit and characterized by an emergent low temperature scale. Panels (a) to (c) taken from Ref. 2 below show the calculated phase diagram in the plane of Josephson coupling vs. scaled shunt conductance for increasing noise power.
- E. Dalla-Torre, E. Demler, T. Giamarchi and E. Altman, Nature Phys. 6, 806-810 (2010)
- E. Dalla-Torre, E. Demler, T. Giamarchi and E. Altman Phys. Rev. B 85, 184302 (2012)
- E. Dalla-Torre, E. Demler, T. Giamarchi and E. Altman arXiv:1205.3496