Ultra-cold atomic systems offer a new laboratory, with truly unique properties, to study the organization of quantum matter. The unique aspects of these sometimes require us to critically revisit central concepts developed in the context of other systems, thus leading to new insights. A few examples from our work on novel equilibrium states of ultra-cold atomic systems are given below.
Topological States in a One-Dimensional Fermi Gas with Attractive Interactions
(with J. Ruhman and E. Berg)
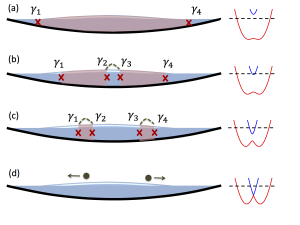 We describe a novel topological state, which forms in a one-dimensional Fermi gas with Rashba-like spin-orbit coupling, a Zeeman field and intrinsic attractive interactions. In spite of having total number conservation (no proximity pairing), Majorana-like zero modes appear in this system and can be linked with interfaces between two distinct phases that naturally form at different regions of the harmonic trap. One phase has gapped single-fermion excitations and in the other they are gapless. As a result, the low lying collective excitations of the system, including the dipole oscillations and the long-wavelength phonons, are doubly degenerate.
We describe a novel topological state, which forms in a one-dimensional Fermi gas with Rashba-like spin-orbit coupling, a Zeeman field and intrinsic attractive interactions. In spite of having total number conservation (no proximity pairing), Majorana-like zero modes appear in this system and can be linked with interfaces between two distinct phases that naturally form at different regions of the harmonic trap. One phase has gapped single-fermion excitations and in the other they are gapless. As a result, the low lying collective excitations of the system, including the dipole oscillations and the long-wavelength phonons, are doubly degenerate.
(With G. refael, A. Polkovnikov, Y. Kafri, R. Vosk and S. Pielawa)
 Still under construction.
Still under construction.(With Achim Rosch and Eugene Demler)
 Under Construction
Under Construction
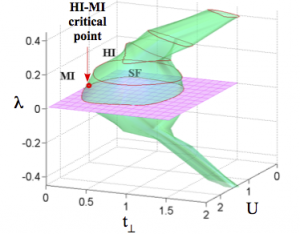 inversion symmetry. Hence in the plane defined by the tuning parameter of the transition (e.g. V) and symmetry breaking there is an isolated gapless critical point at the origin. We have shown that encircling this critical point adiabatically pumps one boson across the system. When multiple chains are coupled, the two insulating phases are no longer sharply distinct, but the pumping property survives. This leads to strict constraints on the topology of the phase diagram of systems of quasi-one dimensional interacting bosons.
inversion symmetry. Hence in the plane defined by the tuning parameter of the transition (e.g. V) and symmetry breaking there is an isolated gapless critical point at the origin. We have shown that encircling this critical point adiabatically pumps one boson across the system. When multiple chains are coupled, the two insulating phases are no longer sharply distinct, but the pumping property survives. This leads to strict constraints on the topology of the phase diagram of systems of quasi-one dimensional interacting bosons.