analysis | Arithmetic variety

If $a$ and $b$ are positive real numbers, if you add $a$ to itself enough times, eventually you will surpass $b$ . This is called the Archimedean property, and it is one of the fundamental properties of the system of real numbers. Informally, what this property says is that no numbers are infinitely larger than others. We can formally define this property as follows:

Let $F$ be an ordered field. We say $F$ is Archimedean if, for $x, y \in F$ where $x, y > 0$ , there exists a natural number $n$ such that $nx > y$ .

An example of a non-Archimedean number system is the hyperreal numbers. Hyperreal numbers are an enlargement of the real numbers that also contain “infinite” and “infinitesimal” quantities. The hyperreal numbers are used to give an alternative formulation of calculus in the subject of non-standard analysis, where instead of using limits, one computes with actual infinitesimals.

More familiar examples of non-Archimedean fields are function fields. For example, consider the field of rational functions (on $\mathbb{R}$ ), denoted $\mathbb{R}(x)$ . We can order rational functions by declaring that

$p > q$ if $p(x) > q(x)$ as $x \to \infty$

for any $p, q \in \mathbb{R}(x)$ . In other words, we order rational functions by looking at their asymptotic behavior. One can check that this satisfies the axioms, making $\mathbb{R}(X)$ an ordered field.

Exercise: Show that a rational function

$p(x) = \frac{f(x)}{g(x)} = \frac{a_nx^n + \cdots + a_1x + a_0}{b_mx^m + \cdots + b_1x + a_0}$

is positive with respect to the order (i.e. $p > 0$ ) if and only if $a_n/b_m > 0$ .

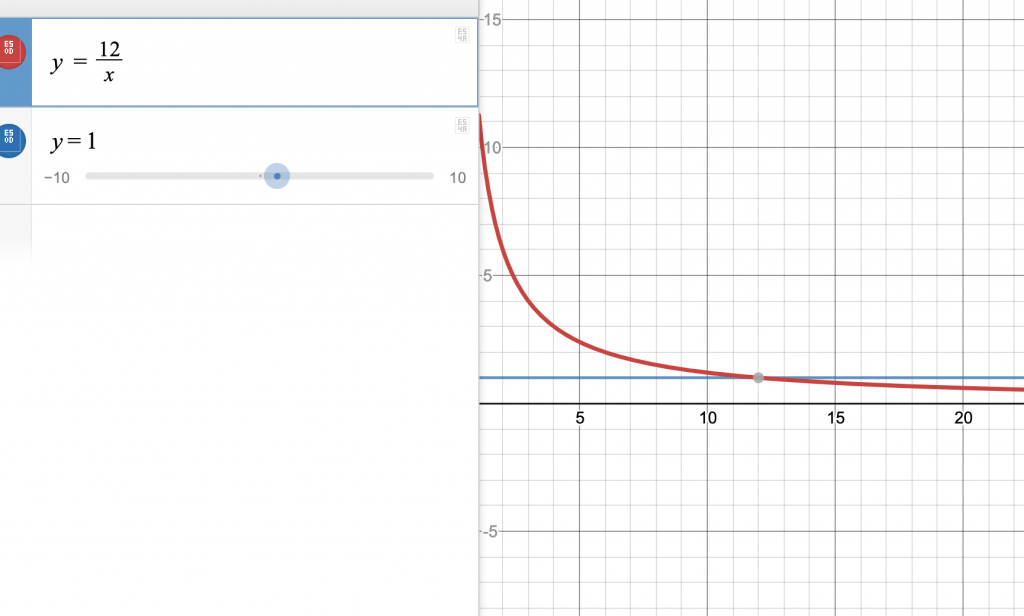
Now one can see that the field of rational functions is clearly not Archimedean. For example, if we consider $p(x) = 1/x$ , no matter how many times we add it to itself, it will never surpass $q(x) = 1$ : the function $np(x) = \frac{n}{x}$ is eventually surpassed by $q(x) = 1$ , no matter how great $n$ is.

Exercise: Define the degree of a rational function to be the degree of its numerator minus the degree of its denominator. For rational functions $p, q > 0$ , show there exists an integer $n$ such that $np > q$ if and only if degree $(p) \geq$ degree $(q)$ .

Thus the basic idea of the Archimedean property is at the core of asymptotic analysis. In defining big-O notation, we write $f(x) = O(g(x))$ if some multiple of $f$ surpasses $g$ as $x$ goes off to infinity.

In the next post, I will discuss the Archimedean property for valued fields (as opposed to ordered fields), and how this applies to number theory.

Arithmetic variety

Category Archives: analysis

The Archimedean property