A complex number is algebraic if it is the root of some polynomial ![]() with rational coefficients.
with rational coefficients. ![]() is algebraic (e.g. the polynomial
is algebraic (e.g. the polynomial ![]() );
); ![]() is algebraic (e.g. the polynomial
is algebraic (e.g. the polynomial ![]() );
); ![]() and
and ![]() are not. (A complex number that is not algebraic is called transcendental)
are not. (A complex number that is not algebraic is called transcendental)
Previously, I wrote some blog posts (see here and here) which sketched a proof of the fact that the sum and product of algebraic numbers is also algebraic (and more). This is not an obvious fact, and to prove this requires some amount of field theory and linear algebra. Nevertheless, the ideas in the proof lead the way to a better understanding of the structure of the algebraic numbers and towards the theorems of Galois theory. In that post, I tried to introduce the minimum algebraic machinery necessary in order to state and prove the main result; I don’t think I entirely succeeded.
However, there is a more direct approach, one which also allows us find a polynomial that has ![]() (or
(or ![]() ) as a root, for algebraic numbers
) as a root, for algebraic numbers ![]() and
and ![]() . That is the subject of this post. Instead of trying to formally prove the result, I will illustrate the approach for a specific example: showing
. That is the subject of this post. Instead of trying to formally prove the result, I will illustrate the approach for a specific example: showing ![]() is algebraic.
is algebraic.
This post will assume familiarity with the characteristic polynomial of a matrix, and not much more. (In particular, none of the algebra from the previous posts)
A case study
Define the set ![]() . We will think of this as a four-dimensional vector space, where the scalars are elements of
. We will think of this as a four-dimensional vector space, where the scalars are elements of ![]() , and the basis is
, and the basis is ![]() . Every element can be uniquely expressed as
. Every element can be uniquely expressed as ![]() , for
, for ![]() .
.
We’re trying to prove ![]() is algebraic. Consider the linear transformation
is algebraic. Consider the linear transformation ![]() on
on ![]() defined as “multiply by
defined as “multiply by ![]() “. In other words, consider the linear map
“. In other words, consider the linear map ![]() which maps
which maps ![]() . This is definitely a linear map, since it satisfies
. This is definitely a linear map, since it satisfies ![]() and
and ![]() . In particular, we should be able to represent it by a matrix.
. In particular, we should be able to represent it by a matrix.
What is the matrix of ![]() ? Well,
? Well, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Thus we can represent
. Thus we can represent ![]() by the matrix
by the matrix
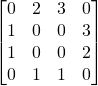 .
.
Now, the characteristic polynomial ![]() of this matrix, which is defined as
of this matrix, which is defined as ![]() , is
, is ![]() , which has
, which has ![]() as a root. Thus
as a root. Thus ![]() is indeed algebraic.
is indeed algebraic.
Why it works
The basic reason is the Cayley-Hamilton theorem. It tells us that ![]() should satisfy the characteristic polynomial:
should satisfy the characteristic polynomial: ![]() is the zero matrix. But the matrix we get when plugging
is the zero matrix. But the matrix we get when plugging ![]() into
into ![]() should correspond to multiplication by
should correspond to multiplication by ![]() ; thus
; thus ![]() .
.
Note that I chose ![]() randomly. I could have chosen any element of
randomly. I could have chosen any element of ![]() and used this method to find a polynomial with rational coefficients having that element as a root.
and used this method to find a polynomial with rational coefficients having that element as a root.
At the end of the day, to prove that such a method always works requires the field theory we have glossed over: what is ![]() in general, why is it finite-dimensional, etc. This constructive method, which assumes the Cayley-Hamilton theorem, only replaces the non-constructive “linear dependence” argument in Proposition 4 of the original post.
in general, why is it finite-dimensional, etc. This constructive method, which assumes the Cayley-Hamilton theorem, only replaces the non-constructive “linear dependence” argument in Proposition 4 of the original post.