Introduction

William James (1842-1910), the great Harvard philosopher and leader of early American psychology, famously defined psychology as "the science of mental life" (in his Principles of Psychology, 1890). The goal of psychology as a science is to describe and explain states of mind -- or, as we would now put it, the mental structures and processes that underlie human experience, thought, and action. Quite simply, the task of psychology is to understand how our minds work, just as the job of physics is to explain how the physical world works, and the job of biology is to explain how living things work, the job of sociology is to explain how societies work, and the job of political science is to explain how political institutions work.

But what exactly does the mind do?

In the 19th century, a group of theorists known as the phrenologists, led by Franz Joseph Gall (1758-1828) and Johann Gaspar Spurzheim (1776-1832) attempted to classify all the things the mind did, and relate each activity to a particular part of the brain. Gall came up with a list of 27 "mental and moral faculties", and Spurzheim added 10 more. The phrenologists distinguished between various kinds of love (physical love, parental love, friendliness), different aspects of perception (form, location, color, tune, and time), different kinds of thinking (comparing and causal reasoning), and various traits and attitudes (wit, secretiveness, benevolence, and conscientiousness). That's a lot of mental functions, and even so the phrenologists got into debates over precisely how many there were. (We'll talk more about the phrenologists in the lectures on the Biological Bases of Mind and Behavior.)

But even before the phrenologists arrived on the scene, a succinct answer was provided by the German philosopher Immanuel Kant (1724-1804), in his famous (and pretty much unreadable) Critique of Judgment (1790):

"There are three absolutely irreducible faculties of mind: knowledge, feeling, and desire".

In other words, mental states consist of the thoughts, feelings, and desires that pass through our minds when we're conscious. It is my virtue of our minds that we acquire and use knowledge, and experience emotions, moods, needs, and wants -- how we know things, feel what we feel, and desire what we desire.  By saying that these states were "irreducible", Kant meant simply that thoughts, feelings, and desires were in some sense independent of each other, and one was not derivative of one or more of the others (this is a controversial point, and not all psychologists accept it, as we'll see in our discussions of emotion and motivation).

In the 20th century, the American psychologist Ernest R. (Jack) Hilgard (1904-2002) recast Kant's three "faculties" as the "Trilogy of Mind" (1980):

So, the scope of psychology is very broad, including:

Why do we care about these mental states? At the very least, we care about them because thoughts, feelings, and desires are things we experience, and we want to know more about them -- just as we want to more about the stars in the skies, the earth beneath our feet, and the other creatures that live here with us.

But more than idle curiosity is at stake here. We want to understand how our minds work because we believe that mental states play a causal role in our behavior. The underlying philosophical rationale for scientific psychology is the doctrine of mentalism, which states in formal terms, that

Mental states are to action as cause to effect.

In other words, that what we do depends on what we think and feel and want.  Understanding how our minds work, why we think and feel and want as we do, then, is essential to understanding why we do what we do.  Psychology is the science of mental life, but it's also one of a number of behavioral sciences like anthropology or economics, political science or sociology.  All the behavioral sciences are concerned with understanding the behavior of human beings and other animals -- how individuals interact with the physical world and with each other.  But each of these behavioral sciences has its own preferred way to explain why we behave the way we do.

For example, consider a rather dramatic behavioral observation: that some person, X, has committed suicide. The question naturally arises: "Why did he kill himself?". Psychology offers three general types of answers for consideration:

A psychological explanation of behavior explains an individual's action by invoking his or her mental states. And psychology, as a science, seeks to understand the nature of these cognitive, emotional, and motivational states: how they relate to each other, how they relate to what is going on in the brain and the rest of the body, and how they relate to the individual's behavior.

Not everyone agrees with this idea, by the way. Some philosophers (and some psychologists, too) dismiss mentalism as mere folk psychology -- a set of naive, traditional ideas about the mind and behavior, unsupported by scientific evidence, that are doomed to be replaced by a more sophisticated, truly scientific view.

The Domain of Psychology

Psychology is a behavioral science, one of a number of disciplines (including anthropology, biology, economics, history, political science, and sociology) that seek to understand how individuals (whether humans or nonhuman animals) interact with each other and the world in which they live. Each of these sciences has a particular scope, and a particular set of concepts by which it seeks to explain behavior. As described above, psychology explains behavior in terms of the individual's mental state -- the organism's thoughts, feelings, and desires.

Herbert Gintis, an economist, has suggested that all the behavioral sciences are united around the following principles:

This is a good start, though we can quibble about some of the points.  Three things, however, are for sure:

Psychology as a Social Science

Psychology is also a social science, because humans are social beings as well as intelligent beings. We live in groups, rather than in isolation, and we cooperate and compete and make exchanges with each other on a daily basis. Our individual mental lives take place in this social context, and so we have to understand it in order to understand what we think, and what we do. Accordingly, psychology must be concerned with a number of problems:

In general, while cognitive psychology studies mind in the abstract, social psychology studies mind in action, or mind in social relations -- how beliefs, attitudes, and other mental states translate into interpersonal and inter-group behavior.

Psychology as a Biological Science

The brain is the physical basis of the mind, and so psychology must also be a biological science. The attempt to understand how the mind works naturally leads to questions concerning the biological basis of mental life --the anatomical structures and physiological processes involved in cognition, emotion, and motivation. Accordingly, psychologists are interested in a number of biological topics, including:

Interestingly, modern biology has an expressly social aspect, ecology, which is concerned with the study of interacting how groups of organisms, such as species, each of which occupies its own environmental niche. Ecology is concerned with the organism's adaptation to its environment, and its relations with other organisms. For humans, mental processes play a crucial role in adaptation and interaction. For this reason, psychology may be viewed as part of an interdisciplinary field known as human ecology.

Psychology as a Physical Science

Because mental life is a result of the activity of the brain, and the brain in turn is an electrochemical system, psychology is also in some sense a physical science. 

Levels of Explanation

The idea of psychology as a physical science, at least in part, raises the question of reductionism -- the idea that the principles of psychology can be reduced to principles of physical science. Such a reduction would allow us to eliminate reference to such "folk-psychological" terms as belief, attitude, and the like, and explain behavior solely in terms of neural functions. The question is whether knowing the physical state of a person's brain will allow us to predict his or her thoughts, feelings, desires, and actions.

The doctrine of reductionism was succinctly stated in a quotation attributed to Ernest Rutherford (1871-1937), a British physicist who won the 1908 Nobel Prize (ironically, in chemistry!) for his work on radiation:

There is only one science, and it is physics; all the rest is stamp collecting.

Reductionism is particularly favored among physicists and psychologists and philosophers who might be diagnosed as suffering from "physics envy", and it remains at topic of considerable debate among psychologists and philosophers.

Here's a nice example of biological reductionism.  Zietsch et al. (2-15) reported a genetic study of marital infidelity -- what the biologists euphemistically call "extra-pair mating".  In a group of more than 7,000 twins and siblings, they calculated that about 53% of the variability in infidelity was due to genetic factors (62% for men, 40% for women), and the rest due to environmental factors.  Moreover, by genetic typing of a subsample of the subjects indicated that infidelity was associated with the presence of any of five variants (technically, single nucleotide polymorphisms) of a particular gene, known as AVPR1A.  Now, Zietsch et al. were very careful not to be reductionistic.  They pointed out that genetic and environmental variance were split about 50-50 (when the two sexes are combined).  And they also pointed out that, while genes might contribute to the motive to be unfaithful, the environment provides the opportunity to do so.  Nevertheless, some commentators immediately jumped to the conclusion that, when it comes to marital infidelity, "our genes make us do it".  For example, writing in the New York Times, Richard Friedman, a prominent psychiatrist, wrote the following ("Infidelity Lurks in Your Genes", New York Times, 05/24/2015):

We are accustomed to thinking of sexual infidelity as a symptom of an unhappy relationship, a moral flaw or a sign of deteriorating social values....  But... it turns out that genes, gene expression and hormones matter a lot....  We have long known that men have a genetic, evolutionary impulse to cheat, because that increases the odds of having more of their offspring in the world.  But now there is intriguing new research showing that some women, too, are biologically inclined to wander, although not for clear evolutionary benefits.  Women who carry certain variants of the vasopressin receptor gene are much more likely to engage in "extra pair bonding," the scientific euphemism for sexual infidelity....  For some, there is little innate temptation to cheat; for others, sexual monogamy is an uphill battle against their own biology.

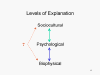
In the final analysis, however, psychology links three different levels of the explanation of behavior: the psychological level, emphasizing the individual's mental states; the sociocultural level, emphasizing social structures and processes external to the individual; and the biophysical level, emphasizing physicochemical structures and processes. The psychological level of explanation has links "up" to the sociocultural level as well as links "down" to the biophysical level, but psychologists must favor explanations of behavior that refer to the individual's mental states.

To return to the example of suicide:

Suicide is very complex.  For an up-to-date overview of the literature, see Suicidal: Why We Kill Ourselves (2018) by Jesse Bering.  And if you're having suicidal thoughts, call the National Suicide Prevention Lifeline at 1-800-273-8255.

 
Each of these levels of analysis is appropriate, and is favored by particular disciplines (sociologists and anthropologists prefer the sociocultural level of analysis, while geneticists and neuroscientists prefer the biophysical level). A biophysical analysis is not superior to a psychological or a sociocultural analysis; the levels are just different. No level is more legitimate than any other, and none carries any special privilege.

However, the three levels of analysis are almost certainly interrelated. For example, a discipline known as sociobiology (a term coined by the evolutionary biologist E.O. Wilson) attempts to account for various sociocultural phenomena directly in terms of biological processes such as evolution by natural selection.

From a psychological point of view, however, the processes studied at the sociocultural and biophysical levels of analysis generally find their pathways to the individual person's behavior through the psychological level. For example, a person's suicidal behavior may reflect his belief in the authority of a charismatic leader or the righteousness of a cause (Japanese kamikaze pilots during World War II, the residents of Jonestown, Guyana, the suicide bombers of the Middle East, or the terrorists of September 11, 2001 come to mind). Alternatively, his feelings of depression may be the product of genetic predisposition, or engendered by certain hormonal changes.

When all is said and done, however, psychology, as the science of mental life, includes all three levels of analysis, and tries to link them together by asking the following sorts of questions:

Psychological explanations of behavior are always at the level of the individual's mental state, but other levels can also be of interest for what they tell us about the mind -- the sociocultural matrix in which the individual resides, and the biological bases of mental life.

The Philosophical Backdrop for Modern Psychology

The questions about mind addressed by scientific psychology have their origins in age-old philosophical questions. These have been summarized as follows by the philosopher Thomas Nagel:

The same sorts of questions were posed in another way by the artist Paul Gaugin (1848-1903), in the title of one of his famous "Tahitian" paintings: Where do we come from? What are we? Where are we going? (1897) Note the baby on the right-hand side of the painting, with the elderly woman on the left.

Historically, psychology is an offshoot of philosophy, addressing these philosophical questions about the mind with the tools of empirical science. (Psychology is an offshoot of physiology as well, as some of the earliest scientific psychologists worked on problems of sensation; but that is another story.)

A Comic-Book History of the Philosophy of Mind

It should be understood that there was a time when nobody, not even philosophers, were asking questions about the nature of the mind. Before the 9th century BCE, questions about mental life weren't discussed by philosophers, at least in the West. Julian Jaynes, in his very provocative book, The Origins of Consciousness in the Breakdown of the Bicameral Mind (1976), notes that there are very few references to consciousness or mental life in early literature (e.g., the Iliad and the Odyssey). To the extent that characters in this ancient literature had thoughts, feelings, and desires, these were not mental acts of the person, but rather things put into his or her mind by the gods.

Around the 6th century BCE, things began to change. Characteristic of the philosophical tradition of the "Golden Age" of Greece (Socrates, c. 469-399 BCE; Plato, c. 427-347; Aristotle, 384-322 BC) was the recognition that people's thoughts, feelings, and desires were their own. This is the origin of consciousness to which Jaynes refers -- the point at which people became aware of the contents of their own minds as such, and also aware of their ability to control these contents themselves. Similar things were happening in Eastern philosophy, by the way: for example, Buddha taught that ideas came from sensations, while Confucius taught that individuals could think for themselves. These were novel, revolutionary ideas at the time.

This philosophical tradition developed further in the West -- first in the hands of certain philosophers of the medieval Christian Church (e.g., Augustine of Hippo, 354-430; Thomas Aquinas, 1225-1274), and later by the philosophers associated with the Enlightenment of 17th and 18th century Europe. The Enlightenment philosophers were particularly interested in the debate over the relation between knowledge and experience. On this question, there merged two fundamental points of view which still divide philosophers, and psychologists, today. 

These and other Enlightenment philosophers posed questions that psychologists now try to settle scientifically, and we will talk about them from time to time in this course. But the Enlightenment philosophers were not ready to pursue a science of mental life. In large part, we owe this reluctance to the doctrine of dualism proposed by Descartes at the very beginning of the Enlightenment period. Descartes held that mind and body were different substances. For example, in contrast to the body, the mind occupied no space. Thus, the argument went, the mind can't be measured; and because science depends on measurement, a science of the mind was impossible.

This position was undercut in the 19th century, with the development of classical psychophysics. Ernst Weber (1840) and Gustav Fechner (1860) measured the relations between physical stimuli and the corresponding sensory experience -- demonstrating, in the process, that sensory experience was not only measurable but lawful. At roughly the same time, Hermann von Helmholtz (1856-1966) was conducting experimental investigations into the mechanisms of spatial perception.

In addition, Franciscus Donders (1868) showed that mental processing could be measured in terms of the time it takes a person to perform a mental operation -- introducing the reaction time or response latency methodology which forms such an important part of modern scientific psychology.

Similar methods were eventually applied to the so-called "higher" mental processes -- including memory, thought, and any other mental function that went beyond immediate sensory-perceptual experience. For example, Hermann Ebbinghaus (1885) invented the nonsense syllable (strings of letters consisting of a consonant, a vowel, and a consonant, such as TUL, that are pronounceable but meaningless) in order to study the formation of associations between ideas -- and, in the process, showed quantitatively how memory was related to experience. At about the same time, Mary Whiton Calkins (1896), invented the paired associate technique, consisting of one nonsense syllable paired with another, to the same purpose. Ivan Pavlov (1898), a physiologist working in Russia, and Edward L. Thorndike (1898), a psychologist working in the United States, pioneered the study of learning in animals. In this way, in the latter quarter of the 19th century, a science of the mind began to emerge.

In the 20th century, psychology broke away from both philosophy and physiology, and established itself as an independent science. For most of this century, psychological and philosophical analyses of mind proceeded somewhat independently. This was partly due to the so-called "behaviorist revolution" in psychology, which began in the late teens and 1920s. The behaviorists, as their very name implies, studiously avoided any reference to mental states (because they can't be publicly observed), and confined their analyses to tracing the relations between observable physical stimuli, and observable behavioral responses.

But questions about mental life didn't go away. They returned to the forefront in the 1950s and 1960s, when the so-called "cognitive revolution" reinstated mind as a -- some would say the -- proper subject matter for psychology. Now, psychologists and philosophers work together, along with linguists, computer scientists, neurologists, and anthropologists, in the interdisciplinary field known as cognitive science.

The Relation of Psychology to Philosophy

Modern philosophy can be divided into four main branches. Logic is concerned with the formal principles of reasoning, and the criteria by which judgments and inferences are to be held valid. Aesthetics has to do with the nature of beauty and art. Ethics has to do with questions of good and evil, moral duty, and obligation. Metaphysics has to do with the fundamental nature of being and reality.

Metaphysics, in turn, has three main branches: ontology, which is concerned with the nature of existence; cosmology, which is concerned with the nature of the universe; and epistemology, which is concerned with the nature of knowledge.

Each of these branches of philosophy has is psychological counterpart.

In addressing questions of mind (or, for that matter, any other question), philosophers use three main methods: introspection, or the detailed inquiry into their own experiences and beliefs; linguistic analysis, or the meanings of words and the ways in which they are used in language; and logical argument, based on principles developed in the study of rational judgment.

There is much to be gained by such efforts. However, even philosophers realize that they are not necessarily adequate to the task of understanding and explanation. In the first place, introspection can be biased by inaccuracies and distortion in perception and memory. Moreover, introspection can only reveal what is consciously accessible, not what might be going on outside of phenomenal awareness. Moreover, there is a difference between the principles that might be postulated on the basis of philosophical principle and those that actually govern human experience, thought, and action. For example, philosophers sometimes assume that people follow the principles of normative rationality when making judgments. That is, they engage in careful calculation of probabilities, according to mathematical logic. However, people are generally poor judges of the probabilities of events. To take another example, philosophers sometimes assume that people follow a principle of utilitarianism in their behavior, maximizing pleasure and minimizing pain; but this tendency is reversed in individuals who are depressed or masochistic.

Like the universe as a whole, the mind cannot be understood by thought and reason alone. Just as astronomers ask empirical questions about cosmology with the tools of their science, so do psychologists ask empirical questions about the mind. The characteristic features of the scientific method in psychology are the systematic observation of events under controlled conditions; observations are collected in formal experiments which test explicit hypotheses derived from some theory; observations derived from these experiments are expressed in quantitative terms, which are then subjected to statistical tests to determine the validity of the investigator's inferences. For more details, see the corresponding Lecture Supplement, "Beyond Impressions: Descriptive and Inferential Statistics".

The Essence of Science

The essential methods of science, whether it's a science like physics or a science like psychology (or, for that matter, a science like sociology) began to emerge about 1000 years ago. In fact, one writer has called the scientific method "The Best Idea of the Millennium" ("Eyes Wide Open" by Richard Powers, 04/18/99). Here's a capsule history of the development of the scientific method, partly inspired by Powers' article.

For a more thorough analysis of the scientific method, see The Scientific Method: An Evolution of Thinking from Darwin to Dewey by Henry M Cowles (2020).  The essence of the scientific method is often presented as a sequence of five steps: observation, hypothesis, prediction, experiment, confirmation.  But as Jessica Riskin, a historian of science at Stanford University, points out in her review of Cowles's book, you could make a reasonable case for almost any of the 120 permutations of these five steps ("Just Use Your Thinking Pump", New York Review of Books, 07/02/2020).  Although the scientific method can be traced back to Bacon and Newton in the 17th century, the term "scientist" itself is very young, having been introduced only in 1834 by William Whewell -- and it didn't catch on until much later in the 19th century (the British Association for the Advancement of Science was founded only in 1831; before that).  Before that, people like Newton and Galileo, and even Darwin, thought of themselves as natural philosophers, and if British natural philosophers were really famous they were members of The Royal Society for Improving Natural Knowledge, which received its royal warrant in 1663.  Cowles concludes that "The rise of 'the scientific method' was less a success than a tragedy", because its "monopolistic claim on transcendent truth" (Riskin's words) set science apart from the humanities. 

The Shift from Authority and Intuition to Observation

The Enlightenment of the 17th and 18th centuries gave rise to a Scientific Revolution in which divine revelation and arguments from authority and intuition were supplanted by the search for universal principles through systematic observation, controlled experimentation, and the mathematization of universal laws (think of Galileo and Newton).

Controlled Experiment

Roger Bacon (1214-1294), an English scholastic philosopher, read Alhazen's work in translation, and developed his point of view into a full-blown philosophy of science based on empirical evidence derived from controlled experiments, in which variables are manipulated one at a time to see which have an effect on some outcome. Aristotle had argued against such experiments, on the ground that the world must be understood as a whole, not in terms of particulars. In his Opus Majux (1267), Bacon discussed four causes of ignorance:

Parsimony

William of Ockham (1290-1349), another English scholastic, promoted another scientific principle, which has come to be known as the Law of Parsimony, or "Ockham's Razor". Given a number of different explanations for a particular outcome, Ockham argued, the simplest explanation is to be preferred over more complicated ones. Ockham fully realized that the universe might be very complex; what he argued against was unnecessary theoretical complication.

"Experimental Philosophy"

With the principles of empirical observation, controlled experiment, and parsimony in hand, the stage was set for the revolution in "experimental philosophy" announced by Francis Bacon (1561-1626; apparently no relation to Roger), another English philosopher. In summing up the scientific method, Bacon sought to banish the four "idols of the mind":

The new science was exemplified by Galileo Galilei (1564-1642), who used the telescope to confirm Copernicus' theory that the Earth revolved around the Sun; William Gilbert (1540-1603), who discovered magnetism; Johannes Kepler (1571-1630), who discovered that the planets travel in elliptical, not circular, paths; and William Harvey (1578-1657), who discovered the circulation of the blood.

Utility of Knowledge

These facts revealed by the new experimental philosophy were all very interesting, if at the time they were not particularly useful. But Francis Bacon also promoted the notion of practical knowledge -- the use of scientific knowledge to improve the condition of mankind. From Bacon we get the idea that "knowledge is power"-- an idea that lies at the heart of our post-industrial "knowledge economy" based on information and information services. But we wouldn't get there for a long time (first we had to have an industrial revolution).

Induction

Francis Bacon also held the view that science progresses by the steady accumulation of empirical facts derived from empirical observation. In this inductive method, facts come first, and theory comes later, induced from the facts, and explaining the facts. To have a theory first smacked of the argument from authority or intuition that both Bacons, Roger and Francis, fought against. Facts, impartially collected, would speak for themselves. Once a theory emerged from the data, however, it was never taken as the last word. It was always subject to continued verification by new evidence, which would confirm or deny it.

The Hypothetico-Deductive Method

The Baconian (and Newtonian) emphasis on observation and induction lasted through the 19th century, and well into the 20th. For example, Charles Darwin ((1809-1882) induced the theory of evolution by natural selection from observations of the geographical distribution of finch beaks and tortoise shells. But in the 20th century, Karl Popper (1902-1994) convincingly argued that induction was insufficient to guarantee true knowledge. To use his example, if all you observe are white swans, you might well conclude that all swans are white, but this conclusion would be disproved by the observation of even a single black swan (like the ones my wife photographed in Melbourne, Australia).  He also pointed out that Einstein's theory of relativity had shown that Newtonian physics, which had been regarded as definitive since the 17th century, was not right.  Accordingly, Popper argued that science should employ a strategy of falsification, seeking evidence that would disprove a hypothesis. Scientific theories generate specific hypotheses, which are tested against data generated by experiments designed to show that those hypotheses are false. Popper described this method as conjecture followed by refutation.  The best hypothesis is the one left standing after all the alternatives have been disconfirmed. For Popper, the difference between a genuine science, like physics, and a pseudoscience, like Marxian economics or Freudian psychoanalysis, is that the propositions of physics can be falsified, while those of psychoanalysis cannot. Popper's arguments for falsification rather than verification won the day, and the logic -- or at least the rhetoric -- of falsification is part of the everyday rhetoric of science.

Popper applied this methodology even to politics, in his book The Open Society.   For Popper, as Colin McGinn put it, science was the model for civilization ("Looking for a Black Swan", New York Review of Books, 11/21/02). Given the evidence of his posthumous collection of essays, All Life Is Problem Solving, it was also the model for life. For Popper, even elementary instances of learning consisted in the generation of a hypothesis, in the form of an expectation, followed by an empirical test of that hypothesis, until the organism settles on a hypothesis that cannot be falsified. Similarly, in politics, policymakers must be open to feedback and criticism from those -- the voters -- who are affected by their policies. 

Lately, the proliferation of the Internet and social networking has led to the rise of a new movement in the social sciences known as "Big Data", involving data sets containing thousands of variables from millions of subjects.  These data sets are then analyzed, mostly by variants of the correlation coefficient, to reveal whatever relationships may exist in the data.  For the most part, the analysis of Big Data is entirely inductive.  That is to say, the analysts do not approach the data with any specific hypothesis in mind, but rather, seek only to explore it to identify any relationships that exist.  As with any exploratory data analysis, the results should not be taken at face value: if p is set at .05, then 5% of the relationships will be "significant" just by chance.  Accordingly, some way has to be found to replicate the analyses -- perhaps by splitting the sample in half and determining whether any relationships observed in one half are also observed in the other half, a procedure known as double cross-validation.

The hazards of a reliance on Big Data was nicely illustrated by an article by Seth Stephens-Davidowitz, an economist, who analyzed the Google database for searches related to depression ("Dr. Google Will See You Now", New York Times, 08/11/2013).  He uncovered a number of potentially meaningful patterns.  For example, searches increase in frequency during the winter and decrease during the summer, and suggested that people prone to depression should consider moving someplace warm.  Cute, but in fact, epidemiological data shows that the incidence of depression in Minnesota and Wisconsin is actually lower than that in Alabama and Mississippi.  Moreover, the result obscures a more important finding, of seasonal affective disorder, a form of depression already well known to psychiatrists. "Big Data" is, essentially, correlational in nature, and correlation is not causation.  Warmth doesn't protect against depression: sunlight does; and it only protects against some forms of depression.  But we'd never know this from an analysis of Google searches; we only know this from careful epidemiological research that tests specific hypotheses.

Science and Democracy

Robert Lawrence Kuhn, host of Closer to Truth: Science, Meaning, and the Future, a PBS television series on science, has argued that "scientific literacy energizes democracy", by fostering a stance of critical thinking, including demanding both evidence for claims made by authorities and political elites, and logical reasoning from evidence to conclusions "Critical thinking is the essence of the scientific method. Knowing the difference between assumption and deduction, and between presumption and proof, can alter one's outlook and transform an electorate. Moreover, Kuhn argues, scientific thinking fosters diversity through "the capacity to respect pluralistic political positions -- the essence of democracy -- since members can understand that no position, not even their own, can be 'proved' to be the correct one with anywhere near absolute certainty" ("Science as Democratizer", American Scientist, 09-10/03).

As Dennis Overbye has written ("Elevating Science, Elevating Democracy", New York Times, 01/27/2009):

The knock on science from its cultural and religious critics is that it is arrogant and materialistic.... Worse, not only does it not provide any values of its own, say its detractors, it also undermines the ones we already have, devaluing anything it can't measure, reducing sunsets to wavelengths and romance to jiggly hormones. It destroys myths and robs the universe of its magic and mystery.

So the story goes.

But this is balderdash. Science is not a monument to received Truth but something that people do to look for truth. That endeavor, which as transformed the world in the last few centuries, does indeed teach values. Those values, among others, are honesty, doubt, respect for evidence, openness, accountability and tolerance and indeed hunger for opposing points of view. These are the unabashedly pragmatic working principles that guide the buzzing, testing, poking, probing, argumentative, gossiping, gadgety, joking, dreaming and tendentious cloud of activity... that is slowly and thoroughly penetrating every nook and cranny of the world....

It is no coincidence that these are the same qualities that make for democracy and that they arose as a collective behavior about the same time that parliamentary democracies were appearing. If there is anything democracy requires and thrives on, it is the willingness to embrace debate and respect one another and the freedom to shun received wisdom. Science and democracy have always been twins.

In 2017, with an American president who routinely lies, misstates facts, and prevaricates, and authorities in some political quarters speak of "personal truth" and "alternative facts", Time magazine ran a cover story asking whether truth itself is dead (04.03/2017).  Not necessarily.  As Frank Wilczek (a Nobel-laureate theoretical physicist) put it: "science plays a vital role in defining the boundaries of rational discourse" because it is the best way we have of determining what is true and what isn't. ("No, Truth Isn't Dead", Wall Street Journal, 06/24/2017).  Wilczek goes on to state that:

In science, the meaning of "truth" is more substantial, and less susceptible to cynical manipulation.  Empirical facts -- that is, experienced events -- are the gold standard of truth....  Science builds on experience, using logic and... working assumptions [like Newton's laws of motion and gravity]....  Yet a hallmark of science is that we spell out and continually check our assumptions -- and, if necessary, modify them.  That discipline keeps science honest, reliable and on-track....  "Truth", in the context of morality, law, and politics, is a very different concept from logical or scientific truth.  In those domains, science, with its cautious attitude, can't provide all the answers.  Different groups of people make different assumptions, which will sometimes lead to very different conclusions.  But when any version of "truth" contradicts scientific truth (let alone empirical truth), sensible people must reject it.

The Cycle of Theory and Evidence

Verification and falsification are both forms of empiricism, but Popper reversed the traditional Baconian position with respect to the relation between theory and evidence. For Bacon, evidence came first, in the form of observations, and theory came later, by induction. For Popper, however, theory comes first: in this way, he is the culmination of a tradition of rationalism that goes back to Rene Descartes, a 17th-century French philosopher, who attempted to derive true knowledge from reason alone (and thus initiated modern philosophy). The scientist first confronts a problem, such as why the earth appears to revolve around the sun or why apples fall off trees. Then, he or she offers a number of theories, or at least hypotheses, as to which that might be the case. Then, he or she proceeds to test these hypotheses, attempting to disconfirm them, and retains as true the one hypothesis that fails to be disconfirmed. "Truth", however, is always provisional: some future observation may disconfirm even this theory. In practice, however, the relation between theory and hypothesis is more complex than this.

Where do Popper's "problems" come from? They exist in the form of puzzling observations that demand some sort of explanation. A lot of scientific research consists in an investigator publishing an observation, or conducting an experiment that is less intended to test a hypothesis than it is to "poke nature and see what happens". From such observational studies, the investigator may then suggest a theory, or at least a hypothesis (see below). He or she may also perform a verificationist test that indicates that the theory/hypothesis is provisionally true, or at least should be taken seriously by others. Later, another scientist may propose a new theory, and perform a falsificationist test that pits one theory against another. But nobody goes to the trouble of testing every conceivable hypothesis against data from an experiment specifically designed to reject that hypothesis. However much scientists embrace the Popperian logic of falsificationism at the level of rhetoric, actual scientific work involves both induction and deduction, both verification and falsification.

A reliance on empirical evidence is the defining feature of science -- more so than controlled exerimentation (evolutionary biologists and cosmologists don't do it), more so than mathematics (Darwin and Mendel didn't use any beyond arithmetic).  In The Knowledge Machine (2020), Michael Stevens, asserts the iron rule of explanation: no matter how appealing a theory might be on other grounds, scientific theories are validated only by empirical explanation.  Scientists may come up with their hypotheses in a variety of ways, including intuitive appeal or mathematical elegance, but when it  comes to testing a hypothesis, the only thing that counts is the data.

By the way, about that word theory. A "theory" is often misinterpreted as mere speculation, as when creationists or proponents of "intelligent design" criticize the theory of evolution as "just a theory". But in science, a theory is an overarching explanatory framework that accounts for a large set of empirical observations, and goes beyond observable facts to make plausible inferences about facts that have not yet been observed. These inferences are hypotheses, and experiments are conducted, one way or another, to reveal new facts that will determine whether these hypotheses are correct. Evolution by natural selection is a theory. So is general relativity. Theories are never tested whole. Rather, theories generate specific hypotheses, which are then tested against empirical data.

Publication

Research unreported is research undone. It is not until scientific findings are made public, so that other investigators can confirm them, and incorporate them into their theories, or refute them (or at least set limits on them), that research is completed. In order to facilitate publication of scientific research, the first scientific journals were founded in the late 17th century -- the Journal des Savants in France (1665), and the Philosophical Transactions of the Royal Society, in England (1667). The first scientific journals devoted to psychology appeared only in the late 19th century:

Transparency

Publication is an important aspect of the transparency of the scientific method. When scientists report their empirical findings, they also describe the method by which those findings were obtained, so that other scientists can repeat what they have done and confirm or disconfirm their observations. This allows scientists to build on each other's work, so that science is a cumulative enterprise. But this also allows others to critique the experimenter's method, and find flaws that, when corrected, might yield different and more valid results. We do not have to have "been there" when the experiment was done. We can understand, and critique, the experiment solely on the basis of the experimenter's report of his method.

Replication

Scientists confirm or disconfirm each other's findings through replication -- that is, one scientist does what another scientist says he did, and sees if she gets the same result.  Actually, there are two kinds of replication:

• direct replication, in which the initial study's methods are repeated as precisely as possible;
• conceptual replication, which depart from the original procedure in various ways, to test a hypothesis that is conceptually related to the original.

Even direct replications are never precisely identical to the original.  An experiment conducted on subjects recruited from Stanford isn't exactly the same as the original conducted on subjects recruited from Berkeley; and one conducted in 2012 may employ subjects who are quite different from those in an original conducted in 1962 -- even if they are all college students.  So "replication" is a matter of degree.  What is really important is that the replication be faithful to the spirit of the original; and follow the letter of the original as closely as possible.

Beginning in the 2010s, psychology and other fields began to face a kind of replication crisis -- which is to say, a number of highly visible experiments failed to be replicated, casting doubts, not just on the original studies, and the researchers who conducted them, but also on the field in general (Pashler & Wagenmakers, 2012).   

• In 2014, the Many Labs (ML) project attempted to replicate 13 effects reported in social psychology journals, 11 of which were successfully replicated (Klein et al., Social Psychology, 2014).  Two effects, which in fact had aroused controversy when first published, failed to replicate
  
• In 2015, the Open Science Collaboration (OSC; Science, 2015) reported the results of 100 attempts to replicate effects reported in 2008 in three prominent psychology journals, representing a wider sample of psychological research.  Only 47% of the replications were deemed successful, in that they yielded statistically significant effects similar to the originals.   
  

At first glance, however, the outcome of the OSC study would seem to impeach the validity of much psychological research, if not psychology in general, but this would be misleading (as noted by Gilbert et al., Science, 2016).  For example, some of the "replications" weren't true replications, in that they departed significantly from the procedures of the original study.  For example, one study of white Americans' stereotypes concerning African-Americans was "replicated" in Italy.  And a study which asked Israelis to imagine the consequences of military service was "replicated" by asking Americans to imagine the consequences of a honeymoon.  These procedural infidelities also occurred in some of the ML "replications" as well.  In fact, replications whose procedures were endorsed by the authors of the original study succeeded 60% of the time, compared to 15% of studies which were not endorsed. 

Still, 60% isn't a great hit rate, either, and does suggest that psychology does faces a kind of replication crisis.

Social Science

From roughly the time of Roger Bacon onward, science has been concerned with understanding the natural world of physics and biology. Under the influence of Descartes' distinction between mind and body, the 18th-century German philosopher Immanuel Kant asserted that there could never be a science of the mind, because the mind was not a physical entity that could be measured. It was not until the mid-19th century that Weber, Fechner, Helmholtz, and other psychophysicists showed that "lower" mental processes such as sensation and perception could be subject to scientific analysis, and only in the late 19th century that Ebbinghaus and others showed that the same was true for "higher" mental processes such as memory. Also in the mid-19th century, August Comte (1798-1857), a French philosopher, showed that science could reveal the workings of social groups as well as the workings of the individual mind. Based as they are on controlled observation and the testing of hypotheses derived from theory, the "social" sciences of sociology, anthropology, economics, and political science are every bit as much sciences as are the "natural" sciences like physics, chemistry, and biology.

Some philosophers of science have claimed that social science can't be real science because it isn't predictive; it can only explain things that happened, in a post-hoc manner.  The sciences are real sciences, because they entail testing predictions in experiments.  This claim is bogus. 

The real difference between the natural and social sciences is that the phenomena of natural science are observer-independent.  Galaxies, tectonic shifts, and hurricanes exist regardless of whether there is anyone to observe them.  But the phenomena of social science are different, because they are observer-dependent: they are the product of human cognitive activity -- of consciousness, if you will.  They don't exist unless there is an observer present to experience -- and construct -- them.  Mountains and molecules have features that are intrinsic to their physics.  But marriage and money depend for their existence on human attitudes: they are what they are only by virtue of agreement between conscious beings.

In this respect, economics may be an intermediate case.  When Adam Smith, in The Wealth of Nations (1776), referred to the "invisible hand", he seemed to imply that the laws of economics -- of supply and demand and so forth -- are observer-independent phenomena that occur regardless of human cognitive activity.  But many of the facts of economics are observer-dependent.  Like currency: a dollar bill is worth a dollar only because someone says it is; as a piece of paper, it has no intrinsic, observer-independent value.  And markets: you can have a capitalist economy, or a socialist economy, or a mixed economy, etc.; one economic system may be better than another, what economy you have depends on someone's choice.  Capitalism isn't in physics.

For a provocative discussion of the status of economics as a science -- a discussion that has implications for psychology -- see:

• "What Is Economics Good For?" by Alex Rosenberg and Tyler Curtain (New York Times, 08/25/2013).
• "Economics as Science" by Eric S. Maskin (New York Times, 08/29/2013),
  
• and the dialogue stirred by Maskin's letter (New York times, 09/01/2013). 

And for that matter, psychology may also be an intermediate case, because it is both a biological science, interested in the relations between mental states and brain activity, and a social science, interested in the relations between mental structures and processes and social structures and processes.  (Psychology is primarily a social science, though, because it is fundamentally concerned with the individual's mental life: his or her knowledge and beliefs, feelings and desires.) 

In the final analysis, however, both economics and psychology are social sciences, because the phenomena they study are essentially human constructions, and their processes can be altered by the very predictions that social scientists make.

Both cases differ from the natural sciences.  In seismology and meteorology, predicting an earthquake doesn't make it happen; and if a hurricane is predicted, nothing can be done to prevent its formation.  That's because earthquakes and hurricanes are observer-independent phenomena.  Financial crises, and individual choices, aren't.

Psychology (on its "social" side) and the other social sciences are sometimes characterized as "soft science", in contrast to allegedly "hard" sciences like physics and chemistry.  But that's a misnomer. As Theodore Lowi, a prominent political scientist, once remarked, "political science is a harder science than the so-called hard sciences because we confront an unnatural universe that requires judgment and evaluation".  The same is true for psychology as a social science.

Big Science

Well into the 20th century, most science was done by individual investigators, often independently wealthy or supported by wealthy patrons. Galileo essentially worked alone; so did Darwin and the Curies. But in the 1930s and 1940s, and especially with the Manhattan Project to build the atomic bomb during World War II, all that changed: now much science is was done by large teams of investigators supported by large government grants. This is certainly true in physics and astronomy, where research into the smallest and largest domains of the universe is conducted enterprises like the Lawrence Berkeley Laboratory (the first national laboratory, was founded by E.O. Lawrence in 1931) using instruments like the Hubble Space Telescope and the proposed Superconducting Supercollider. In biology there is the Human Genome Project, and in medicine there are multi-site clinical trials and large-scale epidemiological studies.

Psychology is also entering into a phase of Big Science, with brain-imaging studies that require whole teams of investigators to carry out -- not to mention "Big Data" based on huge numbers of observations culled from the Internet. Still, even in astronomy, the oldest and most developed of the sciences, there is room for small-scale and even amateur researchers ("In Praise of Amateurs" by Freeman J. Dyson, New York Review of Books, 12/05/02). In psychology, an lone investigator, armed only with a paper-and-pencil questionnaire, desktop computer, and a bunch of willing college students, can make fundamental contributions to the field.

Big Science.  Hallelujah.
Big Science.  Yodellayheehoo
(Laurie Anderson, "Big Science" from United States I-IV, 1983)

The Experimenting Society

Science comes in two forms, basic, interested in knowledge for its own sake, and applied, interested in the application of scientific knowledge to improve human affairs. In the 1960s, the psychologist D.T. Campbell and others proposed that the scientific method be applied to questions of public policy as well as to questions of scientific theory. In this way, public policies could be freed from ideology, and put on an objective, scientific basis. If you think that vouchers improve educational outcomes of inner-city schoolchildren, or that managed care improves the quality of healthcare while lowering its cost, then do the experiment and find out.

Dynamic Systems

Science is concerned with causal explanation -- not just with describing the universe, but also with explaining how it came to be that way. And since roughly the time of Aristotle, our concept of causation has been unidirectional: A affects B, which in turn affects C. However, it's now clear that, in both the natural and social sciences, causality can be bidirectional or reciprocal: A can have an effect on B, but B can also have an effect on A while C can affect both B and A. A situation where everything affects everything else -- or at least could -- calls for a new set of scientific methods. To a great extent, this is what theories of chaos or complexity are all about.

Paradigm Shift

From roughly the time of Roger Bacon onward, the prevailing view of scientific progress is of an incremental, successive, approximation to the truth. We start out with a pretty good theory, which gets refined by more rigorous experiments -- or gets rejected when those experiments fail. Theories are accepted because they have the best evidence supporting them. But in the 1960s, Thomas Kuhn, a philosopher of science trained in physics, argued that that's not how science works at all. From Kuhn's perspective, the competition between theories is essentially a political battle. At any one time, scientific investigation proceeds within a generally accepted view of the world, which Kuhn calls a paradigm, which determines which questions get asked and how they get answered. Knowledge builds up within this paradigm, which Kuhn calls "normal science", until a point comes when research reveals certain anomalous results, which cannot be explained within that framework. At that point a new paradigm emerges, which explains the anomalous results as well as all the results that were consistent with the old paradigm emerges. Kuhn characterizes the competition between the new paradigm and the old one as a period of revolutionary science. Eventually, the new paradigm triumphs over the old one, an event which Kuhn calls a paradigm shift. The Copernican revolution in physics was one such scientific revolution; so was the Darwinian revolution in biology; the rise of chaos and complexity theory may also reflect a paradigm shift.

Science Studies

From roughly the time of Roger Bacon onward, and particularly after Descartes, Western culture has been based on the view that true knowledge can be obtained by observation and reason -- a human-centered view of things known as modernism. However, Kuhn's notion of scientific revolutions implies that scientific revolutions are won and lost not by the data, but by an essentially political process. In his view, scientific revolutions occur not because the new paradigm is empirically better than the old one, but because the proponents of the new paradigm achieve positions of power within the discipline. This means that you can have not just a philosophy of science and a history of science, but also a social science of science, which seeks to understand how scientific research is shaped and constrained by social forces. A lot of scientists don't like this view, because they think that "true" science is objective, and thus independent of socio-political influence. Still, there's something charming about skepticism, which has been at the center of science since the time of Roger Bacon, being applied to science itself. At their core, for all the occasional silliness about physical laws being social constructions, that is what science studies are all about.

Postmodernism

Some social theorists have also taken Kuhn's view to mean that science does not really entail a progressive, successive approximation to truth, but that the various paradigms are each true in their own way -- or, to put it differently, that there are many truths, all equally valid. This is essentially the viewpoint of postmodernism, or post-structuralism. Although postmodernism would seem to be essentially anti-scientific, this is only true when science is confined to the physical and biological spheres. If you jump off a building, you're going to fall no matter what you believe. This is because the Law of Gravity is the same for everyone. But postmodernism has some virtues when applied in the social sciences, because some reality is, in fact, socially constructed. To take a clear example, a dollar bill is worth a dollar for no other reason than that the American government says it is. Many human institutions are purely social constructions, but they are no less "real" because of that fact.

Voodoo Science

Scientific evidence, such as fingerprints and DNA assays, is often used in the courtroom to provide evidence of guilt or innocence. Under the traditional Frye Rule (1928), scientific evidence was admissible if the principle in question -- that fingerprints or DNA are unique, for example -- was generally accepted within the relevant scientific community. But in its 1993 Daubert decision, the Supreme Court left it to individual judges to determine whether a claim is adequately supported by the available scientific evidence. Most judges are not trained scientists, of course, and so the Daubert decision left the problem of distinguishing between genuine and bogus science. Robert L. Park, a physicist, addressed this issue in his book, Voodoo Science: The Road from Foolishness to Fraud (2002). According to Park, here are "The Seven Warning Signs of Bogus Science" (Chronicle of Higher Education, 01/31/03).

Ethics in Research

No matter how interesting or important the question, there are certain studies that scientists simply can't perform, because they're unethical.  Ever since the trial of the "Nazi Doctors" following World War II, international law has recognized that the procedures employed scientific and medical research, including psychological research, must conform ti certain ethical standards.  The standards differ somewhat for basic and applied (medical and psychotherapeutic) research, but the basic principles are these:

1. Subjects must give informed consent to participate in research.
2. Insofar as this is possible, investigators must take care to eliminate any risk that subjects will be harmed by their participation in any research study.
   
3. "Risk" is defined broadly to include not just physical risks, but also psychosocial risks -- e.g., threats to self-esteem or psychological well-being, or harm to a social group of which the subject is a member.
4. Any such risks must be clearly explained to subjects before they agree to participate in the study.
5. To insure compliance, proposed research must be evaluated and approved by an Institutional Review Board (IRB) with the authority to deny permission to an investigator to conduct the study in question.
   

For background on the ethics of human research, particularly medical research, see a pair of articles by Marcia Angell, former Editor of the New England Journal of Medicine, published in the New York Review of Books:

• "Medical Research: The Dangers to the Human Subjects" (11/19/2015).
  
• "Medical Research on Humans: Making It Ethical" (12/03/2015).

Angell traces the deep background of research ethics, beginning with the Nuremberg Code issued in 1947, and subsequent developments, such as the 1964 Declaration of Helsinki published by the World Medical Association and the Common rule issued by the US Department of health and Human Services in 1991, and also discusses more recent cases.  Angell is a physician, so most of her discussion is focused on medical research, such as the ethics of placebo-controlled studies.  But her general points are applicable to psychological and other behavioral-science research as well.

One important difference between basic psychological research, and applied medical and psychotherapeutic research, is that the "subjects" in applied research are often patients seeking treatment for some illness or disease (such as cancer or schizophrenia), and they often volunteer for research (such as clinical trials) in the hope that they will receive effective treatment for whatever their illness is.  Insofar as basic psychological research is concerned, the primary rule is that psychological experiments are "episodic".  That is, there is the assumption that the subjects who participate in them will not be changed by virtue of their participation.  They might be a little richer, by virtue of compensation for their participation, and they might be a little more knowledgeable about some aspect of psychology; but they'll leave the experiment "the same person" as they were when they arrived.  

Where Psychology Fits

Because the brain is the physical basis of mind, psychology is a natural science, closely tied to biology. But because human thought and action takes place in a social context, psychology is also a social science. In some sense, psychology links the social sciences to the biological science, through its emphasis on the experience, thought, and action of the individual human organism. Either way, psychology is a science, just like biology and sociology. Social science studies a social reality that may differ from one society to another, but that doesn't make social science unscientific. Social scientists share with their colleagues in the physical sciences the basic Baconian virtues. As Bertrand Russell put it (somewhere):

It is not what the man of science believes that distinguishes him, but how and why he believes it. His beliefs are tentative, not dogmatic; they are based on evidence, not on authority or intuition."

For more on what science is and what it isn't, how it works and how it doesn't, see UCB's "Understanding Science" website.

A Capsule History of Psychology

The pioneering 19th-century psychologist Herman von Ebbinghaus remarked that

"psychology has a long past, but only a short history".

The "long past" reflects more than 2,500 years of philosophical inquiry into cognition and other matters of mind, going back at least as far as the ancient Greeks. The word psychology is, of course, derived from the Greek psycho, referring to the "soul" or the "mind", and the Latin logia, or "study". The word was first used (in German) to refer to the "study of the soul" or of spirits", as a kind of theological discipline. But by the early 18th century, the German philosopher Christian Wolff was using the term in roughly our modern sense. The word first occurs in English in writing by the British philosopher David Hartley, who defined psychology as "the theory of the human mind", a branch of natural philosophy.

But all of this early psychology was strictly philosophical in nature, based on introspection, reasoning, and logical inference, not on the systematic collection of empirical evidence.

The "short history" is due to the fact that psychology as a scientific enterprise only began to develop in the 19th century. Why, if people have been interested in how their minds work for so long, did psychology emerge as a science so long after physics, chemistry, biology, and other natural sciences?

From Philosophical Psychology to Scientific Psychology

In large part, the delay in the emergence of psychology as an independent science is attributable to the French philosopher Rene Descartes (1596-1650), who in the 17th century articulated a philosophical position known as dualism. According to Descartes, body and mind were composed of two different substances, the first material in nature, and the second immaterial. Based on this doctrine of dualism, the 18th-century German philosopher Immanuel Kant argued that psychology could never be a science, because science was based on measurement and the mind, being immaterial, could not be measured. Thus, during the Enlightenment, when other sciences were developing rapidly, psychology was ruled out of the scientific enterprise by definition.

Nevertheless, less than half a century after Kant, a fully quantitative psychology began to emerge with studies of sensation and perception.

A Catalog of "Firsts"

At this point, scientific psychology began to develop rapidly

First Laboratories

The decisive step away from both philosophy and physiology was the establishment of laboratories for the study of mental life.

Actually, a claim could be made that Harvard had the first psychology laboratory in the world, because James had already installed some laboratory apparatus in the Philosophy Department beginning as early as 1875; but James disliked experimentation, and didn't really go beyond classroom demonstrations to conduct formal experiments; so the honor of the first working American psychology laboratory goes to Hall at Hopkins).

First Textbooks

For the first half-century or so, scientific psychology was represented by individual journal articles and specialized monograph studies.  Eventually, however, psychologists began to assemble the emerging body of scientific research and theory into comprehensive textbooks.

Actually, a case can be made that the first comprehensive textbook of psychology, covering cognition and emotion, and including personality and social psychology, was Kant's own Anthropology, which appeared in 1798 (Hatfield, 1798; Kihlstrom, 1998.  By "anthropology", Kant meant "knowledge of mankind", which for him included the mind as well as culture.  But Kant's book was based on his own personal experience, and rational analysis, not the kind of controlled empirical research represented in Wundt's and James's texts.  It is perhaps more properly considered the last textbook of philosophical psychology.  But it's an interesting book nonetheless, and well worth dipping into.

First American PhDs

As the science developed, an increasing number of scholars undertook graduate study in psychology, as opposed to philosophy or physiology.

First Journals

At first, psychological research was published in journals of philosophy, like Mind, and in general scientific journals, like Nature and Science, but as the literature burgeoned, universities and publishers began to sponsor specialized journals devoted to psychology.

First Organizations

As psychology began to be accepted as a scientific enterprise, psychologists began to organize themselves as an academic discipline.

A Whig History of Scientific Progress in Psychology

In much the same way that Immanuel Kant believed that scientific psychology was impossible, Wilhelm Wundt believed that scientific psychology, while possible, was limited to the study of immediate experience -- that is, to sensation and perception.  This is because he believed that it was important, scientifically, to tie mental experience to the physical conditions of stimulation, and to the physiology of the nervous system.  In this view, the so-called "higher" mental processes, such as memory and thought, were not susceptible to experimental investigation. They were too far away, as it were, from the instigating physical stimulus; and the underlying physiology was to complex. 

Accordingly, Wundt distinguished between two kinds of science:

Nevertheless, just as Weber and Fechner proved Kant wrong about measuring the mind, beginning in the 1980s a number of pioneering psychologists about the possibility of investigating "higher" mental processes, increasingly distant from both physical stimuli and physiology.

Reflecting the concerns of Cartesian "modern" philosophy, most early experimental psychology was focused on knowledge, and the means by which it is acquired through experience -- sensation, perception, learning, memory, and thinking.  But experimental psychology also took up  the other two aspects of the Kantian trilogy of mind.

All of this work was focused on how the mind operates in general -- the basic principles of cognition, emotion, and motivation that apply to everyone. But quite quickly, psychologists began to be interested in individual differences in mental function -- that is, how people might differ from each other.

Along with the IQ test, one of psychology's most visible products was the development of questionnaire methods for the assessment of personality and attitudes.

The development of techniques for the assessment of social attitudes was a major milestone in the development of social psychology, but so was the introduction of the controlled experiment.

At this point, by the mid-1930s, personality and social psychology emerged full-fledged as a quantitative, experimental science of individual mental life in its social context.

Schools of Psychology

When scientific psychology began, it was organized into "schools" of investigators who shared certain assumptions and methods (now called paradigms), often centered on particular individuals.

The first of these was structuralism, associated with Wundt at Leipzig, and also with his student, E.B. Titchener, at Cornell. Like Wundt, the structuralists were focused on immediate experience, meaning problems of sensation and perception. They got their name from their assumption that complex experiences could be analyzed into constituent, simple elements -- a kind of mental chemistry.

In the late 19th century, structuralism had its principal American rival functionalism, associated with William James (always at Harvard), John Dewey (first at Chicago, then at Columbia), and James Rowland Angell (first at Yale, then at Chicago). The functionalists were much influenced by Darwin's theory of evolution: whereas for the structuralists mind just existed, as a thing to be analyzed, for the functionalists mind had a purpose -- to aid in adaptation to the environment.

In the early 20th century, a third school, known as behaviorism, sprung up around John B. Watson (at Hopkins), and, later, B.F. Skinner (first at Minnesota and Indiana, and later at Harvard). The behaviorists were troubled by the fact that conscious experience was inherently private, whereas science should be based on public observation. Accordingly, they redefined psychology: it was no longer the science of the mind, as James had defined it, but rather a science of behavior. The behaviorists, as their very name implies, studiously avoided any reference to mental states (because they can't be publicly observed), and confined their analyses to tracing the relations between observable physical stimuli, and observable behavioral responses.

But questions about mental life didn't go away. They returned to the forefront in the 1950s and 1960s, when the so-called "cognitive revolution" overthrew the behaviorist revolution and reinstated mind as a -- some would say the -- proper subject matter for psychology. Cognitive psychology is now central to scientific psychology.

Psychology in Interdisciplinary Inquiry

Psychology is an independent scientific discipline, derived from neither biology nor sociology, and that stands at the nexus of the biological and social sciences. At the same time, psychologists participate in a number of interdisciplinary fields of inquiry that are concerned with various aspects of mind and behavior.

Psychology and Cognitive Science

Psychology is a component of a broad interdisciplinary field known as cognitive science, which takes as its subject matter the acquisition, representation, and use of knowledge by minds and brains, machines and societies. The various fields in cognitive science are represented by the "cognitive hexagon" presented in a report to the Sloan Foundation, which provided early financial support to various academic programs in cognitive science, including the one at Berkeley:

For an historical introduction to cognitive science, see The Mind's New Science: A History of the Cognitive Revolution by Howard Gardner (1985).The image at left, above, is Gardner's original depiction of the cognitive hexagon. The image above and to the right is an adaptation of the cognitive hexagon which serves as the logo for UCB's Cognitive Science Students Association, which includes majors in the undergraduate interdisciplinary Cognitive Science program as well as students from other departments.

Psychology is certainly a cognitive science, because it is concerned with the acquisition, organization, and use of knowledge -- in short, with human intelligence. As a cognitive science, psychology is concerned with a variety of problems:

Historically, cognitive science emerged at a time when psychology, under the influence of radical behaviorism (see above), abjured mentalistic concepts. Cognitive science is interested in more than human mental functioning -- for example, some approaches to artificial intelligence take no interest in "how the mind does it". Still, so far as understanding human mental functioning is concerned, cognitive science does nothing that psychology is not capable of doing so as well, and had it not been for the aberration of behaviorism might never have been developed.

Psychology's status as a cognitive science stems, in part, from the historical preoccupation of philosophers with problems of knowledge. But psychology is not just a cognitive science, because there is more to the mind than cognition. Remember Kant's "three irreducible faculties, and Hilgard's "trilogy of mind"?

So psychology is also an affective science, concerned with emotion, as well as a conative science, concerned with motivation. This was what James was getting at when he defined psychology as the science of mental life in its entirety, and what Hilgard meant when he reminded us that emotion and motivation were also part of mental life.

Psychologists, cognitive scientists, and neuroscientists sometimes use the term "cognitive" to refer broadly to all mental states, including emotion and motivation. But strictly speaking, the term cognitive refers to mental states of knowledge and belief, associated with perception, memory, thought, and language.

In some sense, cognitive science is broader than psychology, because it includes fields like philosophy, linguistics, and anthropology, that approach behavior from other perspectives. But in another sense, psychology is broader than cognitive science, because it encompasses emotion and motivation as well as cognition.

Psychology and Neuroscience

Psychology is also a component of another interdisciplinary field of inquiry, neuroscience -- which also got its start, and its name, in the early 1960s. Before that there was just neurology, a term dating from the 17^th century, neurophysiology (first appearing in English in 1859), and neuroanatomy (1900).

As a biological discipline, neuroscience was initially organized into three branches: molecular and cellular neuroscience, concerned with neurons and other elementary structures of the nervous system -- the whole legacy of what Elliot Valenstein (2005) has called "the war of the soups and the sparks"; then there was systems neuroscience, concerned with how the various pieces of the nervous system connect up and interact with each other; and behavioral neuroscience, concerned with everything else -- but in particular with motor activity, basic biological motives such as hunger and thirst, and the operation of sensory mechanisms -- mostly without reference to mental states as such.

But pretty quickly there began to emerge a fully integrative neuroscience (Gordon, 1990), concerned with making the connections between the micro and the macro, the laboratory and the clinic, and between neurobiology and psychology.

First to make its appearance was cognitive neuroscience, concerned with the neural bases of cognitive functions such as perception, attention, and memory. As with cognitive science, some practitioners of cognitive neuroscience defined "cognitive" broadly, so as to include emotional and motivational processes as well -- really, any internal state or process that intervened between stimulus and response. But, again strictly speaking, cognitive neuroscience is concerned only with the neural substrates of cognitive processes such as perception, attention, memory, thought, and language.

Psychology also contributes to a third interdisciplinary field, sensory science, which attempts to understand how the special senses -- vision, hearing, etc. -- work. This endeavor involves psychologists, physicists, biologists, biochemists, and engineers who devote themselves to the study of optics, acoustics, and the chemical senses (smell and taste).

By analogy with cognitive science and cognitive neuroscience, a new interdisciplinary field, affective science (or, sometimes, affective neuroscience; see below), has emerged to address questions about emotional life. The idea that there should be such an effort, separate from but parallel to cognitive science, implicitly reflects an acceptance of Kant's idea that cognition and emotion are irreducible faculties of the mind. Politically, it is also an attempt to break the hegemony of the cognitive in psychological analyses.

There isn't a conative neuroscience yet, interested in human motivation, though a lot of behavioral neuroscience is interested in eating, drinking, sexual, and parenting behavior in nonhuman animals).

But there is already a field of social neuroscience.

All this neuroscience testifies to our ability, at long last, to uncover the neural substrates of mind and behavior. At the same time, the emergence of behavioral, cognitive, sensory, affective, and social neurosciences underscores the value and status of psychology, which is interested in both cognition and emotion, as well as motivation, the individual and the social context. It seems unlikely that a complete understanding of either cognition or emotion can be obtained without some appreciation of the other. If so, cognitive and affective sciences will be necessarily incomplete approaches to the mind, and cognitive and affective scientists might just as well be psychologists instead.

However, just as not all psychologists are interested in biology (biology is a tool for psychology, but it is not an obligation, and many psychologists do their work without ever thinking about how the brain operates), not all neuroscientists are interested in the mind (some are interested in purely biological questions about how the brain and the rest of the nervous system works, variants called molecular, cellular, and developmental neuroscience, but which are hard to distinguish from plain neurobiology). Even so, many neuroscientists use techniques developed in the psychological laboratories to ask purely biological questions about the nervous system.

Some psychologists are so taken by the possibilities of modern neuroscience -- brain imaging and all the rest -- that they have redefined themselves as neuroscientists.  That's fine, if that's what they want to do, but sometimes they seem to forget that the neuroscience that interests them depends utterly on psychology.  That is because they are interested in the neural basis of mental life, and psychology is the science whose job it is to describe mental life in the first place.  If the psychological description is wrong, the neuroscience will be wrong as well.  As I have put it (2010):

Psychology without neuroscience is still the science of mental life; neuroscience without psychology is just the science of neurons.

Applications of Psychology

Psychology has intellectual value because it contributes to our knowledge of ourselves and our place in the universe. But it also has social value, because it can be applied in the service of human adaptation: to help people to cope with the demands of their physical and social environments, and to actualize their potential as human beings. Using psychological knowledge to change ourselves, and our environments, we can better satisfy our needs, wishes, and hopes.

Thus, psychology is not just an academic, intellectual exercise; it is concerned with application as well.

Through application, scientific psychology can be used to promote and improve human relations (the relations between people), human engineering (the relations between people and the machines they use), and human ecology (the relations between people and their surrounding environment).

The Place of Psychology in Human Inquiry

Most students entering college intend to take the introductory psychology course, even if they have no intention of majoring in psychology, and for good reason.  In 1998, the American Association of Colleges and Universities defined a liberal-arts education as one which "fosters a well-grounded intellectual resilience, a disposition toward life-long learning, and an acceptance of responsibility for the ethical consequences of our ideas and actions".  So defined, "liberal arts" is independent of any discipline, and covers everything from English Literature to civil engineering -- if properly taught and studied.  But certainly, psychology -- understanding our minds and how they work, and why we do the things we do -- is central a a liberal-arts education.

In fact, it can be argued that psychology stands near the center of human inquiry, at the intersection of the natural sciences, social sciences, humanities, and arts.

Steven Weinberg, a Nobel laureate in physics, has written that "the effort to understand the universe is one of the very few things that lifts human life above the level of farce, and gives it some of the grace of tragedy". Whereas literature and the arts are concerned with individual experiences and expressions, psychology is interested in discovering generalizable laws governing human mental life and behavior. Whereas other natural and social sciences study the universe outside the individual, psychology studies what Morton Hunt (1993) has called "the universe within" the individual mind.

Further Reading

For an excellent, nontechnical, historical overview of psychology, see Hunt, M., The Story of Psychology (Doubleday, 1993). For a more technical history with emphasis on American contributions (essentially, a combined history and introductory text), see Hilgard, E.R., Psychology in America: A Historical Perspective (1987).

For short essays on a wide variety of psychological topics (great bedtime or bathtub reading), see Gregory, R. (Ed.), The Oxford Companion to the Mind (1987).

For a short history of Western philosophy, out of which scientific psychology grew, see Kenny, A., (Ed.), The Oxford History of Western Philosophy (Oxford University Press, 1994). For a more technical introduction to the modern philosophy of mind out of which scientific psychology emerged, see Flanagan, O., The Science of the Mind (2nd Ed.).

For an essay on developments in psychology from 1967 (when I took introductory psychology) to 2017 (when I taught my last intro course and retired from the University), see "50 Years of Psychology: A Personal Look Back a "Intro".

This page last revised 12/22/2021.